Multiplication et produit de deux nombres entiers.

La multiplication dans l’ensemble des entiers naturels N est une opération qui, à deux
nombres a et b, associe un autre nombre appelé produit de a et b, noté a x b.

Par exemple, le produit de 4 et de 5 se note 4 x 5. L’opération est la multiplication, le
nombre 4 x 5 s’appelle le produit des deux nombres.

La commutativité de la multiplication.

Il y a une coutume pour lire ce nombre, souvent 4 x 5 est lu 4 fois 5. Le langage courant
a tendance à s’appuyer sur le sens de la lecture de gauche à droite.

Il y a pourtant une autre coutume, (souvent utilisée en sciences) ainsi, 5 +5 +5 +5 ne
comporte que le nombre 5 (ce qui colle bien avec « 4 fois 5 »). Aussi, certaines
personnes écrivent plutôt cette somme en privilégiant le nombre 5 que l’on voit et
l’écrivent en premier. Le produit est écrit alors 5 x 4 et lu « 5 multiplié par 4 » (4 est le
multiplicateur) ou « 4 fois 5 » (ce qui correspond également au fait que 4 est le
multiplicateur).

La somme de 4 nombres égaux à 5 est appelée addition itérée car elle utilise le même
nombre répété. Dans ce contexte, 5 est le nombre que l’on voit (le nombre qui est itéré),
4 ne se voit pas directement dans l’écriture additive (c’est le nombre d’itérations).

Les deux écritures (4 x 5 et 5 x 4) sont cependant correctes pour évoquer aussi bien 5 +
5 + 5 + 5 que 4 + 4 + 4 + 4 + 4, puisqu’elles représentent le même nombre (en
l’occurrence qui est aussi 20).

4 x 5 = 5 x 4 = 5 + 5 + 5 + 5 = 4 + 4 + 4 + 4 + 4 = 20.

Pour dire que 4 X 5 = 5 X 4, on dit que la multiplication est commutative. On dit que 4
est multiplié par 5 ou que 5 est multiplié par 4 indifféremment dans un contexte
mathématique.

La résolution de problèmes.

Ces appuis sur le langage courant ou bien sur le nombre que l’on voit peuvent être
trompeurs du point de vue mathématique. En fait, l’écriture du produit, en
mathématiques, est indifféremment 4 x 5 ou 5 x 4 puisque les deux résultats sont
identiques et représentent le même nombre. Les énoncés de problèmes, bien sûr,
privilégient une écriture plutôt que l’autre, car les énoncés de problèmes s’expriment à
l’aide du langage courant. Avec les élèves, il faut donc être clair dès que l’on écrit la
solution d’un problème et leur faire comprendre très rapidement que les deux écritures
sont possibles et égales car le contexte est alors mathématique. On dit en
mathématiques que la multiplication est commutative.

En ce qui concerne la résolution de problèmes, il faut distinguer l’interprétation de
l’énoncé et ce qui est mobilisé pour la résolution du problème. La solution étant obtenue
dans le contexte mathématique, les écritures 4 x 5 OU 5 x 4 conviennent quel que soit le
contexte du problème (aussi bien pour chercher le nombre de billes contenues dans 5
sachets de 4 billes que dans 4 sachets de 5 billes).

Ce produit noté 4 x 5 ou 5 x 4 (les deux écritures pouvant être associées aussi bien à
4+4+4+4+4 qu’à 5 + 5 + 5 + 5) peut s’obtenir par un calcul (résultat mémorisé ou
résultat retrouvé en appui sur un produit connu, par exemple 4 x 4, ou encore par une
addition itérée) ou bien en s’appuyant sur une représentation schématisée : nombre
d’objets contenus dans des paquets identiques ou encore nombre de carreaux de grilles
rectangulaires.

Interprétation géométrique du produit de 2 entiers.

La commutativité de la multiplication est particulièrement mise en évidence sur les grilles
rectangulaires. C’est pour cette raison que l’utilisation de telles grilles dans le travail sur
cette opération à l’école élémentaire est particulièrement adaptée. De plus, ce contexte
peut se révéler utile lors de la présentation de la technique opératoire traditionnelle.

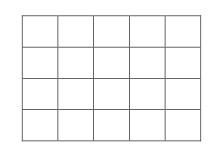
Le produit de 5 par 4 peut s’illustrer comme ci-dessus, c’est alors le nombre de carreaux
d’une grille rectangulaire de 5 colonnes et 4 lignes ou comme ci-dessous par le nombre
de carreaux d’une grille rectangulaire de 4 colonnes et 5 lignes.

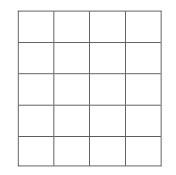
Le produit 5 x 4 est visiblement égal au produit 4 x 5 ; en effet, les deux grilles ci-dessus
ont le même nombre de carreaux, puisqu’elles peuvent être superposées.

2° cas : Multiplication de nombres rationnels en écriture fractionnaire ou avec
une écriture à virgule.

Définition :

Le produit de nombres en écriture fractionnaire (que ce soit des nombres décimaux ou
des nombres rationnels non décimaux) est un nombre dont une écriture fractionnaire a :

• pour numérateur, le produit des numérateurs.
• pour dénominateur, le produit des dénominateurs.

Par exemple :

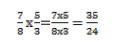
Cependant, cette écriture peut être réduite avec une simplification dans bien des cas.
Si l'on souhaite connaître le produit 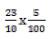il est égal à ou à c'est-à-dire

Remarque :

Cette définition permet de définir également le produit de nombres décimaux.

Par exemple : 0,52x23,5 = 12,220 car 52x235= 12200

Interprétation géométrique du produit.

Le produit de deux nombres décimaux s’interprète comme pour les entiers naturels
géométriquement, comme ci-dessous, en liaison directe avec la notion d’aire.

Le produit de 3,25 par 5,5 est égal au produit de 13 quarts par 11 demis. Ce produit est
aussi l’aire du rectangle ci-dessus avec pour unité d’aire un grand carreau carré. Si l’on
effectue le produit de fractions, on obtient 143 huitièmes. Le résultat est l’aire du
rectangle avec pour unité le petit carré situé en bas, à droite !! Il y en a bien 143 en
tout.

Remarques :

Pour ce qui concerne l’emploi des nombres décimaux, il convient de relever des difficultés
spécifiques.

1. Lorsque dans un problème, on a à calculer le produit d’un décimal par un entier, le cas le plus simple se produit lorsque le multiplicateur est entier. Ainsi, il est plus facile pour un enfant de calculer le prix de 5 stylos à 1,75€ le stylo, que de calculer le prix de 1,75kg de pommes à 5€ le kg.
2. Le cas le plus complexe se produit lorsque le multiplicateur est un nombre inférieur à 1 : dans ce cas, on obtient un résultat inférieur au multiplicande (par exemple 35 x 0,70 est inférieur à 35). Cela est en complète contradiction avec l’idée fréquente qu’un enfant se fait de la multiplication : une multiplication agrandit.

Marie-Christine Marilier