Présentation de quelques erreurs commises par les élèves lors des calculs posés
de la multiplication et de la division de deux entiers naturels.
Les élèves éprouvent souvent des difficultés à effectuer les calculs posés de la
multiplication et de la division car ces techniques requièrent de nombreuses compétences
concernant la numération décimale mais également les autres opérations telles que
l’addition et la soustraction. De plus, plusieurs de ces opérations doivent être faites
mentalement ce qui complique encore les choses.
Les erreurs qui concernent la gestion des retenues dans la technique de la multiplication
trouvent leur origine dans le fait que les élèves ne maîtrisent pas le sens de ce qu’ils font
et ajoutent souvent la retenue au chiffre des dizaines du nombre à multiplier par
exemple.
Exemple d'erreur :
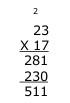
L’élève fait 3 fois 7 font 21, je pose 1 et je retiens 2, puis 2 et 2 font 4 et 4 fois 7 font
28, d’où le résultat 281. Puis il effectue le deuxième produit de 23 par 10 et fait
l’addition. Il s’agit d’une erreur relative à la numération de position et à sa signification.
Une autre erreur consiste à ne pas décaler les calculs de la deuxième ligne lors du calcul
du deuxième produit.
Exemple :
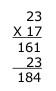
Cette erreur peut être due à une mauvaise maîtrise de la numération de position, mais
plus souvent elle résulte d'une perte de sens dans le calcul : l’élève oublie qu’il multiplie
le premier nombre par des dizaines (par 10 dans l'exemple ci-dessus) et non par des
unités.
Enfin, d’autres erreurs classiques sont liées à la méconnaissance des tables d’addition et
de multiplication, ce qui explique environ les deux tiers des résultats erronés. En ce qui
concerne la technique de la division, en plus des erreurs de calcul dues à une mauvaise
gestion de la multiplication et de la soustraction, une autre erreur classique consiste dans
l’oubli d’un zéro au quotient dans des opérations du type :
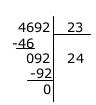
Lorsque le premier reste dans le calcul est 0 et que le chiffre suivant (ici le 9) est trop
petit pour pouvoir effectuer la division, les élèves abaissent le chiffre suivant (ici le 2) et
poursuivent la division sans redonner du sens aux chiffres utilisés. Ici, on ne peut pas
partager les 9 dizaines du dividende en 23 donc le quotient doit indiquer qu’il y a 0
dizaine. Les 9 dizaines du dividende sont ensuite converties en unités et on a alors 92
unités à partager en 23 ce qui fait 4 unités au quotient. De plus, une prise en compte de
la signification du chiffre 2 du quotient aurait pu permettre de comprendre qu’il s’agissait
de 2 centaines et non de 2 dizaines puisqu’on venait de partager 46 centaines en 23. Un
travail portant soit sur l’estimation, soit sur le nombre de chiffres du quotient peut
permettre d’éviter ce genre d’erreur. En effet, si on effectue mentalement la division de
4600 par 20 on constate que le quotient est de 230 et non de 23. De même, si on
considère qu'il faut commencer par diviser 46 centaines par 23, on sait que le chiffre 2
est celui des centaines et que deux autres chiffres sont donc attendus au quotient.
Il est donc indispensable de s’assurer de la maîtrise de l’addition et de la soustraction
ainsi que de la maîtrise de la numération de position et des tables de multiplication avant
de commencer un quelconque apprentissage des techniques opératoires de la
multiplication et de la division.
Françoise Cerquetti-Aberkane, Marie-Christine Marilier