Expressions algébriques
Calcul littéral, équations, inéquations, systèmes.
Introduction :
L’arithmétique utilise au collège seulement les nombres et les 4 opérations sur ces mêmes nombres. L’algèbre, elle, utilise des lettres qui représentent des nombres. Ces nombres sont tantôt fixes tantôt variables.
1) Le statut des lettres en mathématiques
Les lettres de notre alphabet ou de l’alphabet grec, sont utilisées en mathématiques dans des contextes différents, par exemple :
- en géométrie, pour nommer les points, A, B, et C peuvent être les trois sommets d’un triangle. Pour les points, nous avons l’habitude d’utiliser le début de l’alphabet et les majuscules. Le triangle peut être fixe ou variable. Les points A, B, C peuvent être donnés, fixes ou variables. Dans un cas, le triangle est un triangle particulier, dans l’autre le triangle variable est dit quelconque.
- Dans les formules, comme le périmètre du cercle :, les lettres n’ont pas le même statut. R est le rayon de n’importe quel cercle, la
lettre R représente un nombre positif variable, la lettre (pi) par contre désigne un nombre « bien connu » qui ne change jamais et qui a une valeur fixe voisine de 3,1413….
- Enfin, ce dont tout le monde se souvient : oui ! on utilise souvent la lettre x, mais la aussi, elle n’est pas toujours utilisée de la même façon.
Si on écrit 2x+3=1 et que x est un nombre que l’on cherche on dit que x est une inconnue.
Si on écrit x 5 x et bien là, il s’agit d’une fonction, d’une relation, entre tout nombre et un autre nombre qui est le nombre de départ multiplié par 5. On ne cherche pas x, on le fait varier.
2) Méthode arithmétique ou méthode algébrique
Le calcul algébrique ou calcul littéral (calcul avec des lettres qui représentent des nombres) a été introduit pour résoudre des problèmes qui étaient difficiles ou impossibles à résoudre autrement. Il permet souvent de passer de cas particuliers à la généralité ou de démontrer une conjecture.
Le calcul littéral permet de :

Voici un problème :
Résolution arithmétique :
On peut faire un tableau pour tâtonner :

J’ai trouvé tout de suite, comme une enfant. En effet, les enfants prennent souvent la moitié du nombre indiqué qui ici est la réponse. Ce que font également, les enfants c’est de prendre le nombre qui est écrit ici 100.
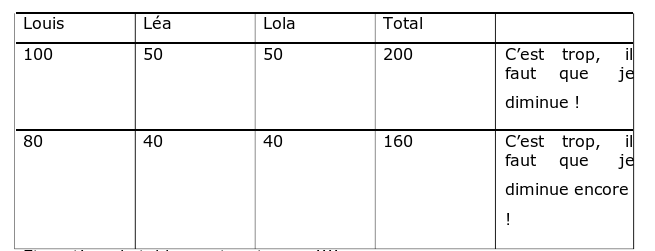
Et continue le tableau, et on trouve !!!!
La résolution algébrique se présente de la façon suivante :
Si on appelle x la part de Louis, alors celle de Léa vaut 0,5x et celle de Lola aussi. La somme des trois parts vaut 100 bonbons, et on peut l'exprimer ainsi : x + 0,5x + 0,5x = 100.
On a donc trouvé une équation traduisant les données du problème, et il nous reste donc à la résoudre, c'est à dire à trouver la valeur de x.
x + 0,5x + 0,5x = 2x, devient 2x = 100. Pour trouver x, il faut diviser les deux membres de l'équation par 2, et x = 50 et les parts de Léa et Lola sont de 25 bonbons.
3) Transformer les expressions algébriques
On a besoin de savoir transformer des expressions algébriques pour résoudre des équations.
a) Transformation de sommes
2x+ 3x peut se réduire en 5x
2x + 3 ne peut se réduire !
b) Transformation de produits Il s’agit du carré de x.

Il y a aussi la double distributivité :
• dans un produit de deux parenthèses : (x + 3)(2x + 1),
et dans ce cas chacun des termes de la première parenthèse sera multiplié à chacun des termes de la deuxième, ce qui va donner ici :
c'est à dire 2x² + x + 6x + 3, que l'on réduit à 2x² + 7x + 3
On peut se retrouver avec un signe – devant une parenthèse devant un signe "-" : - (x - 2)
alors en retirant les parenthèses, on change le signe de chaque terme, c'est à dire ici : -x + 2
attention !
- (x + 1)(2x + 3) (lorsqu'il y a un - devant un produit de parenthèses, mieux vaut effectuer ce produit, et en changer les signes à la fin, ici - (2x² + 5x + 3),
puis en changeant les signes : -2x² - 5x - 3)
Cas particulier : dans un carré : (x + 2)²
cela revient à écrire (x + 2)(x + 2), et à développer,
ou bien à utiliser une identité remarquable pour accélérer l'écriture du développement :
(a + b)² = a² + 2ab + b²
(a - b)² = a² - 2ab + b²
(a + b)(a - b) = a² - b²
Remarque : Il ne faut pas confondre équations et expressions algébriques !
c) Résolution d’équations du premier degré avec une seule inconnue x
ax+b=c
Par exemple 2x+3 = 5 ;
devient
2x +3 -3 = 5 – 3 ;
qui donne 2x = 2 d’où x=1
4) Systèmes de deux équations à deux inconnues
Ici les deux inconnues (le prix d'un croissant et celui d'un pain au chocolat) ne dépendent pas l'une de l'autre, et on va donc poser deux inconnues, x (prix du croissant) et y (prix du pain au chocolat). Si on traduit les données de l'énoncé à l'aide de x et de y, cela donne :
4x + 2y = 5,20
2x + 3y = 4,60
Je vais trouver la valeur des inconnues l'une après l'autre, en éliminant temporairement l'une des deux.
Il y a pour cela deux méthodes :
• la méthode par combinaison
on combine les deux équations pour faire disparaître x ou y
par exemple ici, en retirant deux fois la 2ème équation de la 1ère, on obtient :
4x + 2y = 5,20
-
4x + 6y = 9,20
-------------------------
0x - 4y = - 4
les x ont disparu donc on peut trouver la valeur de y : - 4y = - 4 donc y = 1
ensuite pour trouver la valeur de x on remplace y par 1 dans l'une des équations, ce qui nous donne en choisissant la première par exemple : 4x + 2 = 5,20, donc 4x = 3,20, donc x = 0,80.
Un croissant coûte 0,80€ et un pain au chocolat 1€.
• la méthode par substitution
on exprime une inconnue en fonction de l'autre grâce à une des équations et on remplace dans l'autre équation.
Ici par exemple, on a d'après la 1ère équation : 2y = 5,20 - 4x, donc y = 2,60 - 2x
Donc en remplaçant y par 2,60 - 2x dans la 2ème équation, j'obtiens : 2x + 3(2,60 - 2x) = 4,60,
Donc 2x + 7,80 - 6x = 4,60, et on obtient -4x = -3,20, donc x = 0,80,
et en remplaçant x par 0,80 dans la 1ère équation, on retrouve y = 1.