1) Pourcentages
On peut voir la notion de pourcentage de deux façons soit le pourcentage est un nombre, soit un coefficient de proportionnalité :

- Un pourcentage est une façon d’exprimer un nombre comme une
« fraction de dénominateur cent » ce qui se traduit par 25%=25/100=0,25.
- La notion de pourcentage fournit également un moyen d’exprimer une proportion, en choisissant un référent simple : 100.
Les formulations suivantes sont équivalentes : 25 pour 100, 50 pour 200,
5 pour 20, 250 pour 1000, 1 pour 4, etc.
Cette équivalence se traduit par les égalités :

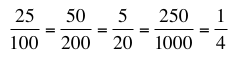
Il y a deux suites de nombres proportionnelles (les numérateurs et les € dénominateurs).
Voici par exemple une résolution de problème où la référence 100 est bien utile :

Quelques problèmes relatifs aux pourcentages
Problèmes de pourcentage simple ou d’application d’un pourcentage :

-Appliquer un pourcentage
Exemple : Si 20% d’une population de 750 personnes lisent un quotidien, quel est le nombre de lecteurs ? (réponse : 150 lecteurs)

-Calculer un pourcentage
Exemple : si 150 personnes sur 750 lisent un quotidien, quel est le pourcentage de lecteurs ? (réponse : 20%)

-Retrouver une quantité à laquelle a été appliqué un pourcentage
Exemple : Les 150 lecteurs d’un quotidien représentent 20% de la population interrogée. Combien de personnes sont interrogées ? (réponse : 750)

Problèmes d’augmentation et de diminution en pourcentages

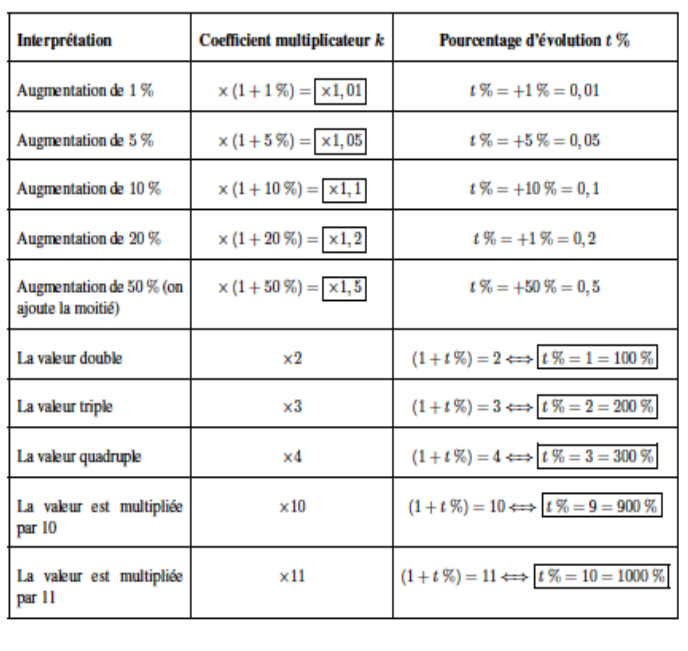
2) Vitesse d’un mobile
Si on considère un mobile ( vélo, automobile, avion, fusée etc...) qui se déplace régulièrement (par exemple une automobile avec régulateur de vitesse), on dit que son mouvement est uniforme et dans ce cas, sa vitesse est constante.

Ici, la vitesse de cette automobile est de 120km/h.

Vitesse moyenne

On a donc les relations : d=vt,             v=dt,          t=dv
d représente la distance parcourue,
v la vitesse moyenne sur le parcours considéré,
t la durée du parcours.
Attention, il est nécessaire d’utiliser des unités cohérentes, par exemple :
- d en km, t en h, v en km/h,
- d en m, t en s, v en m/s.

3) Échelles
On représente une réalité physique (terrain, voiture etc.) par un dessin ou une maquette établie en respectant les proportions.
Cela signifie que toutes les dimensions représentées ont été multipliées par le même nombre.

Il y a donc proportionnalité entre les dimensions dans la réalité et les dimensions sur la représentation de cette réalité.