Les rationnels, les décimaux et les irrationnels
Les nombres rationnels
1) Définition
Un nombre rationnel est un nombre qui peut s’écrire sous forme de quotient
![]() , où a est un entier relatif et b un entier relatif non nul.
, où a est un entier relatif et b un entier relatif non nul.
On dit à l’école primaire que ![]() est une fraction quand a et b sont tous les deux positifs.
est une fraction quand a et b sont tous les deux positifs.
On lit « a sur b » ou bien « a-bièmes » quand b est supérieur à 4,
exemple ![]() se lit quarante-sept cent vingt-cinq ièmes.
se lit quarante-sept cent vingt-cinq ièmes.
a est appelé le numérateur et b est appelé le dénominateur.
Remarque 1 :
Tout nombre entier, relatif ou naturel, est un rationnel car on peut l’écrire
n = ![]()
Remarque 2 :
Une fraction prend du sens pour les élèves progressivement de l’école puis au collège.
A l’école primaire les aspects cardinal et ordinal de la fraction sont introduits.
L’enseignant à partir du partage en parts égales, (aspect cardinal) donne du sens à l’écriture fractionnaire.
L’introduction de la droite graduée où on place les fractions est une façon de travailler l’aspect ordinal de la fraction.
Au collège, la fraction prend le statut de nombre avec l’introduction des opérations et l’utilisation des fractions avec les
autres nombres dans les problèmes.
2) Fractions égales
Un nombre rationnel peut être représenté par une infinité de fractions égales.
On a 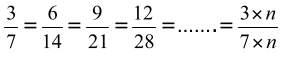 .
.
Propriété
On obtient une fraction égale à une fraction donnée en multipliant ou en divisant le numérateur et le dénominateur de la fraction par un même nombre non nul.
Une conséquence : le produit en croix
Si 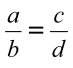 alors A*D=D*C et inversement si A*D=D*C alors
alors A*D=D*C et inversement si A*D=D*C alors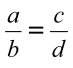 .
.
3) Simplifier une fraction revient à diviser son numérateur et son
dénominateur par un même nombre non nul.
4) Fraction irréductible
Une fraction irréductible est une fraction que l’on ne peut pas simplifier.
Les nombres décimaux
Un nombre décimal est un nombre qui peut s’écrire sous la forme d’une fraction (appelée fraction décimale) à termes entiers et dont le dénominateur est une puissance de 10.
Une fraction décimale peut s’écrire sous la forme ![]() .
.
Tout nombre décimal peut s’écrire sous forme d’une fraction décimale ou d’une fraction irréductible de la forme 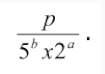 .
.
Un nombre décimal est un nombre qui peut s’écrire à l’aide d’une virgule
et dont la partie décimale contient un nombre fini de chiffres non nul.
Remarque :
- Un nombre entier est un nombre décimal.
- Un nombre décimal est un nombre rationnel.
- Donc, un nombre entier est un nombre rationnel.
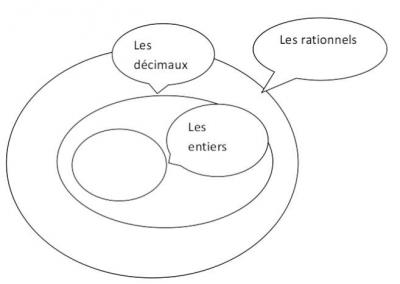
Voici un schéma qui se comprend de la façon suivante :
- un nombre entier est un nombre décimale.
- un nombre décimal est un nombre rationnel.
- un nombre entier est un nombre rationnel.
Propriété commune aux entiers, aux décimaux et aux rationnels :
ILS ONT TOUS une écriture à virgule périodique (quelque chose, des chiffres qui se répètent):
Pour les entiers elle est de la forme :
abcd,00000000000...000000
Pour les décimaux, elle est de la forme :
abcd, nmpqrs00000000000000
Pour les rationnels, elle est de la forme :
abcd,mnpqr..mnpqr..mnpqr...
Les nombres irrationnels
Il existe des nombres qui ne s’écrivent pas à l’aide de quotient, on les appelle des irrationnels.
Les irrationnels ont une écriture à virgule NON périodique.
Le nombre pi, noté par la lettre grecque du même nom Π (toujours en minuscule), est le rapport constant 1 entre la circonférence d’un cercle et son diamètre.
Le nombre Π est aussi le rapport € constant entre l’aire d’un disque et le carré de son rayon.
Mais Π est un nombre irrationnel, c’est-à-dire qu’il n’est pas le rapport de deux nombres entiers.
La transcendance de Π établit l’impossibilité de résoudre le problème de la quadrature du cercle :
il est impossible de construire, à l’aide de la règle et du compas seulement, un carré dont la surface est rigoureusement égale à la surface d’un disque donné.
π ≈
3,14159265358979323846264338327950288419716939937510582
0974944592307816406286208998628034825342117068.....
Devinette :
Trouver le lien entre les décimales de ce nombre et le poème ci-dessous
Que j’aime à faire apprendre un nombre utile aux sages !
Immortel Archimède, artiste, ingénieur,
Qui de ton jugement peut priser la valeur ?
Pour moi ton problème eut de pareils avantages.
Jadis, mystérieux, un problème bloquait
Tout l’admirable procédé, l’œuvre grandiose
Que Pythagore découvrit aux anciens Grecs.
Ô quadrature ! Vieux tourment du philosophe
Insoluble rondeur, trop longtemps vous avez
Défié Pythagore et ses imitateurs.
Comment intégrer l’espace plan circulaire ?
Former un triangle auquel il équivaudra ?
Nouvelle invention : Archimède inscrira
Dedans un hexagone ; appréciera son aire
Fonction du rayon. Pas trop ne s’y tiendra :
Dédoublera chaque élément antérieur ;
Toujours de l’orbe calculée approchera ;
Définira limite ; enfin, l’arc, le limiteur
De cet inquiétant cercle, ennemi trop rebelle
Professeur, enseignez son problème avec zèle
Devinette :
Pourquoi peut on dire que les nombres suivants sont des
valeurs approchées du nombre Π : 3,14 ; 3,1416 ; 22/7 ; 355/113 ?
Chaque mot du poème correspond à une décimale du nombre Π .
Il suffit de compter le nombre de lettres de chaque mot.