Conseil : Attention, ne pas confondre, chiffre et nombre !
- Quel est le chiffre des dizaines de 2011?
- Quel est le nombre de dizaines de 2011?
- Quel est le chiffre des centaines de 2011?
- Quel est le nombre de centaines de 2011?
- Combien de nombres de 3 chiffres peut-on écrire en utilisant une fois et une seule les chiffres 5, 8, 9?
- Combien de nombres peut-on écrire en utilisant les chiffres 5, 8, 9 si cette fois on peut utiliser plusieurs fois le même chiffre?
- Combien de nombres de 4 chiffres peut-on former en utilisant une fois etuneseule les chiffres, 0, 1, 2, 3?
- Choisir un nombre de 3 chiffres différents dont aucun chiffre n’est 0. Renverser son écriture. Calculer la différence entre les deux nombres obtenus. Recommencer 3 fois. Que remarquez-vous ? Comment généraliser?
- Ecrire tous les nombres entiers naturels obtenus en utilisant les chiffres représentés par les lettres c, d, u. Il y en a6.
Calculer avec les lettres la somme S de ces 6 nombres. Diviser cette somme S par c + d + u.
Que remarquez-vous ? Est-ce toujours vrai ? Pourquoi ?
- Ecrire votre année de naissance, faire la somme des chiffres qui la composent puis enlever le résultat obtenu à votre date denaissance. Vous obtenez un multiple de 9.
En est-il de même si on prend une autre date ?
Expliquer si cela reste vrai pour n’importe quelle date de naissance ?
Réponses :
- Le chiffre des dizaines est le 2° en partant de la droite. C’est1.
- Le nombre de dizaines est le nombre de paquets de dix que l’on peut faire avec 2011 objets, ici c’est 201. Ici nombre de dizaines signifie le nombre de groupements de dix que l’on peut faire avec 2011 objets. En effet, 2011=201x10+1.
- Le chiffre des centaines est le 3° en partant de la droite c’est0.
- Le nombre de centaines est le nombre de paquets de cent que l’on peut faire avec 2011 objets. C’est 20, en effet2011=20x100+11.
- Il y a en tout 6 nombres:
deux qui commencent par 5 : 589, 598,
deux qui commencent par 8 : 859, 895,
deux qui commencent par 9 : 985, 958.
- Si on compte les nombres avec le chiffre 5, écrit une, deux ou trois fois on obtient 13 solutions : 555, 558, 559, 585, 595, 855, 955, et les 6 réponses précédentes. On peut obtenir autant de nombres en faisant le même raisonnement avec 8 puis
9. En tout, 6+7+7+7= 27 solutions. Autre raisonnement possible :
pour le premier chiffre, 3 choix possibles pour le deuxième chiffre, 3 choix possibles, pour le troisième chiffre, 3 choix possibles. En tout, 3x3x3= 27 nombres différents.
- On peut faire un arbre de choix pour les compter:
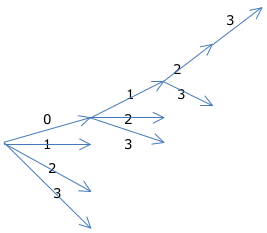
Chaque flèche représente un chiffre : 0, 1, 2, ou 3.
Le nombre de flèches diminue car on cherche les nombres sans répétition des chiffres.
Commençant par 0, nous avons 6 nombres.
Même chose avec les nombres qui commencent par 1, par 2 et par 3. On cherche des nombres à 4 chiffres. Les nombres qui commencent par 0 ont seulement 3 chiffres.
La réponse est donc 18. On ne compte pas les nombres qui commencent par 0.
- 321-123=198
654-456=198
736-637= 99
On obtient à chaque fois un multiple de 11, c’est à dire un nombre divisible par 11 (le reste est nul).
Pour généraliser on écrit avec c>u pour que la différence soit un entier naturel :
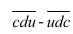= 100c+10d+u-100u-10d-c = 99c-99u=99(c-u) c’est un multiple de 11 mais c’est aussi un multiple de 99.
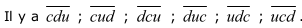
On met une barre au-dessus des lettres pour ne pas confondre avec un produit. En algèbre, quand entre deux lettres, il n’y a rien, cela signifie que les nombres représentés par les lettres sont multipliés.
S=100c+10d+u+100c+10u+d+100d+10c+u+100d+10u+c+100u+10d+c+100u
+10c+d= 100c+100c+10c+10c+c+c+100d+100d+10d+10d+d+d+100u+100u+10u+10u+ u+u=222c+222d+222u=222 (c+d+u)
S divisé par c+d+u donne toujours 222.
- Exemple : Votre année de naissance est 1988
1988 a pour chiffres 1, 9, 8, 8 la somme des chiffres est 1+9+8+8 = 26. 1988- 26=1962. 1962=9x218 c’est bien un multiple de 9.
Prenons une autre date de naissance 1984-(1+9+8+4)=1984-22=1958 =9x162. Dans le cas général, votre année de naissance, à moins que vous soyez très jeune,
commence par 19…, j’appelle d le chiffre des dizaines et u le chiffre des unités,
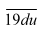-(1+9+d+u)=1000+900+10d+u-10-d-u=1890+9d=9 x (210+d) qui est bien un multiple de 9. C’est donc toujours vrai, nous l’avons démontré.