Une progression des solides aux figures planes.

Il peut être intéressant, au cycle 2, de partir de l’analyse de solides pour retrouver les figures planes, comme le montre cette séquence de travail pour la dernière année du cycle 2, avec une progression allant du cube au carré.

Étape 1 :

Matériel : des solides, de même couleur, de différentes formes : pavés, cubes, prismes, boules, cylindres, polyèdres non parallélépipédiques (manipulables par les élèves).

Chaque solide est repéré par une lettre, le professeur choisit l’un d’entre eux, inscrit sa lettre sur un papier. Les élèves, par groupes de 4, doivent préparer des questions à poser au professeur pour retrouver quel est ce solide. Les réponses ne peuvent être que oui ou non.

Questions et réponses sont écrites au tableau. Quand un groupe est sûr du solide, le professeur confronte leur réponse à ce qui est écrit sur le papier. Au bout de deux ou trois parties, c’est un des élèves qui peut choisir un objet en le montrant aux autres et le
professeur qui pose des questions pour introduire le vocabulaire adéquat et éventuellement certaines questions auxquelles les élèves peuvent ne pas avoir pensé. Puis l’activité est reprise ensuite comme au départ.

Étape 2 :

Matériel : une boule de terre à modeler pour chaque élève.

Les enfants sont invités à faire un cube. La plupart sont insatisfaits de leur construction, l’enseignant leur demande en quoi (« les faces ne sont pas plates, les coins ne vont pas, le cube est penché etc. »), ce qui les conduit à préciser les caractéristiques du  cube : faces planes, « coins » droits, régularités.

Étape 3 :

Matériel : si possible un cube par élève, tous les cubes n’étant pas de même taille. Du papier et des ciseaux.

Si la remarque n’en a pas été faite auparavant, le professeur pose la question : « Est-ce que toutes les faces du cube sont  pareilles ? Comment en être sûr ? »

Des méthodes différentes sont expérimentées (empreinte d’une face, vérification que les autres faces ont la même empreinte, mesurage des côtés).

À l’issue de la mise en commun, tous les élèves dessinent puis découpent l’empreinte d’une face, la plupart des enfants y reconnaissent un carré, ce que confirme l’enseignant par la définition : un carré est une face de cube.

Étape 4 :

Elle a pour but de faire découvrir et expliciter par les élèves que le carré a 4 côtés de même longueur et également de mettre en évidence que respecter cette propriété n’est pas suffisant pour tracer un carré.

Matériel :

- un cube témoin (non disponible pour les élèves), une feuille sur laquelle est dessinée un « morceau » de carré correspondant à une face du cube précédent, un des côtés étant dessiné entièrement et l’autre seulement amorcé (voir ci-dessous).

- un double-décimètre

- des cubes dont les faces sont de dimension différente du carré à reproduire (à disposition des élèves).

Dans un premier temps, les élèves sont invités à formuler des remarques sur les propriétés du carré en réponse à la question :      « Tout à l’heure, je vous demanderai de terminer le dessin d’un carré sur une feuille blanche. À quoi devrez-vous faire bien
attention ? » Comme pour le cube, le professeur demande aux élèves de justifier leurs affirmations. Ayant déjà construit des carrés sur quadrillage, par opposition au rectangle, les élèves connaissent la propriété d’égalité des mesures des côtés qu’ils peuvent prouver là par mesurage ou par pliage de leur carré de papier. Mais n’ayant pas eu jusqu’ici à contrôler les angles puisqu’ils sont donnés par le quadrillage, cette propriété n’apparaît pas.

Au CE1, tous les élèves ne réussissent pas la construction, par exemple les quadrilatères produits n’ont pas tous les côtés de même longueur ou d’autres qui vérifient cette propriété ne sont pourtant pas superposables aux faces du cube !

L’exploitation des productions se déroule en trois temps :

• débat autour des réalisations pour savoir si elles sont correctes ou non : certains arguments font allusion au non respect de la longueur des côtés, d’autres à l’inclinaison des côtés adjacents (trop penché, trop écarté.) ;
• validation par superposition avec le cube témoin, ce qui permet de visualiser « ce qui ne va pas » ;
• formulation des propriétés qui doivent être respectées : longueur des côtés, « coins » droits (le terme angle droit peut être introduit) correspondant à ceux des faces des cubes remis aux élèves (qui pourront ensuite servir de gabarits).

Étape 5 :

Reprise de l’activité avec d’autres carrés à terminer (dont l’enseignant possède un témoin).
Les élèves disposent du même matériel (cubes divers, doubles-décimètres).

Exemples de figures à compléter pour obtenir un carré (selon les compétences des élèves) :

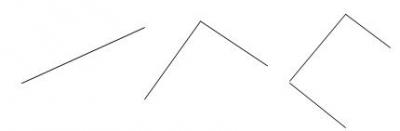
Étape 6 :

Elle a pour objectif de renforcer chez les élèves la nécessité de contrôler les «coins» de la figure à tracer.

Matériel :

Pour chaque équipe : une dizaine de figures découpées dans du papier, de longueurs de côté différentes : des carrés, des losanges aux angles nettement différents de l’angle droit, des losanges et des rectangles proches de carrés.

Il s’agit de classer ces quadrilatères.

La distinction rectangle / non rectangle est facile, en référence à la comparaison des longueurs de côtés. Par contre, la classification des différents losanges amène des discussions : les losanges aux angles très différents de l’angle droit sont bien mis à part (« ils ont les coins pointus et larges »), mais pour les autres, les avis sont partagés. Le professeur propose d’utiliser les cubes pour le savoir. Par superposition, les faux carrés sont alors reconnus, « leurs coins ne sont pas tous pareils » alors que c’est le cas pour les carrés.

Documents d’accompagnement des programmes de mathématiques de l’école primaire.
Ministère de l’éducation nationale Février 2005 p 76 et 77
Ministère de l’Éducation nationale