Exemples de problèmes à l’aide du tangram.
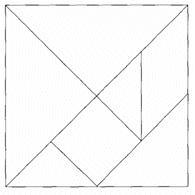
Le Tangram est un ancien jeu chinois.
Il se compose de sept pièces qui peuvent se juxtaposer pour former un carré :
- 5 triangles rectangles et isocèles de trois tailles différentes, nous dirons petit, moyen et grand
- un carré
- un parallélogramme
Le but du jeu est de reproduire une forme donnée, généralement choisie dans un recueil de modèles. Les règles sont simples : on utilise toujours la totalité des pièces, qui doivent être posées à plat et ne pas se superposer.
Un grand nombre de figures géométriques peuvent être reproduites, mais certaines sont très représentatives des rapports mathématiques et géométriques liant les différents éléments. Une réflexion sur certaines figures permet d'en déduire des théorèmes géométriques d'une façon visuelle.
Plusieurs problèmes sont possibles selon le modèle :
- modèle de type 1 taille réelle avec le contour de la figure à réaliser.
- modèle de type 2 (aide pour les élèves) à la taille réelle des pièces, avec quelques pièces dessinées.
- modèle de type 3 avec le contour de la figure à réaliser, mais en taille réduite ou agrandie.
Voici quelques exemples de réalisation avec leurs solutions. Si l’on veut les utiliser on ne donnera aux élèves que le contour de la réalisation et non le contour de toutes les pièces.

En utilisant son imagination, on peut inventer autant de motifs et de figures que l'on veut : silhouettes d'animaux, formes humaines, caricatures, objets divers, etc. On peut aussi résoudre un problème donné, par exemple reproduire une forme complexe dont on a seulement le contour. La troisième façon de jouer consiste à travailler sur des problèmes géométriques posés par les sept pièces du jeu.
Le tangram ci-dessus peut être utilisé avec plusieurs objectifs mathématiques :
On peut travailler :
- les formes géométriques planes et leurs propriétés.
- le glissement et le retournement (activité importante pour travailler la symétrie orthogonale).
- les aires et périmètres de quelques figures géométriques.
Exemple de problème (niveau facile).
Objectif : Observer les formes géométriques planes et leurs propriétés.
Matériel : Par élève, les 7 pièces du tangram ou de tout autre puzzle géométrique.
- Demander aux élèves de réaliser un animal, un personnage ou tout autre chose avec toutes les pièces du puzzle utilisé.
- Garder la trace des réalisations des élèves en n’en prenant que le contour, et également sur une autre feuille la solution. Au cours d’une autre séance, distribuer ces traces aux élèves et leur demander de les refaire. On peut aussi utiliser à ce stade, des réalisations du commerce et fournir aux élèves des modèles à taille réelle sur lesquelles ils pourront poser leurs pièces. Prévoir des aides possibles que les élèves pourront prendre s’ils ne trouvent pas, sur lesquelles figureront le dessin d’une puis de deux pièces etc.
- On peut ensuite donner aux élèves des réalisations à reproduire en leur donnant cette fois-ci des modèles de contour à taille réduite ou agrandie. Procéder de la même façon en prévoyant des aides pour ceux qui se découragent ou ne trouvent pas.
Remarques :
Il vaut mieux utiliser un puzzle avec moins de pièces que de donner aux élèves, tout de suite, le contour de chaque pièce car, en ce cas, le problème est souvent trop simple à résoudre. Il n’y a plus de résolution de problème.
L’intérêt du tangram est qu’il comporte une pièce qui n’a pas d’axe de symétrie, le parallélogramme. Cette pièce doit donc être retournée pour réaliser certaines formes. On pourra donc choisir un autre puzzle ayant les mêmes caractéristiques afin de favoriser le retournement des pièces, par exemple le méli mélo (1) ci-dessous :
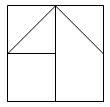
Ce puzzle comprend 5 pièces un carré, 3 triangles rectangles isocèles et un trapèze rectangle. Cette dernière figure n’a pas d’axe de symétrie et doit donc être retournée pour faire certaines réalisations. On pourra d’ailleurs utiliser ce puzzle également en cycle
3 car les activités sur les aires et périmètre peuvent être pratiquées de la même façon.
Exemple de problème de géométrie cycle 3.
Objectifs :
- Observer et utiliser les formes géométriques planes et leurs propriétés.
- Utiliser le glissement et le retournement (activité importante pour travailler la symétrie orthogonale.
- Préciser les notions d’aires et de périmètres.
Matériel : Un tangram construit et découpé dans du carton épais (environ 8cmx8cm) de la même couleur recto et verso.
(Des feuilles de papier pointé à maille carrée)
Problème : Construire des polygones en utilisant certaines pièces du tangram et comparer leur aire et leur périmètre.
- En utilisant les deux petits triangles rectangles isocèles du tangram, chercher des polygones, en particulier des triangles et des quadrilatères. Insister sur le carré, le triangle rectangle isocèle et le parallélogramme (on peut obtenir deux parallélogrammes si on retourne les pièces).
- Demander aux élèves de dessiner sur papier quadrillé ou pointé les figures obtenues et de les nommer.
- Faire la même chose avec d’autres figures du tangram sans nécessairement les utiliser toutes.
- Demander aux élèves de comparer dans différents cas, les aires des polygones réalisés ainsi que leurs périmètres. Il est possible d’utiliser les figures réalisées sur papier quadrillé. On peut choisir le petit triangle isocèle comme unité de mesure et donc calculer pour chaque pièce du tangram son aire en fonction de cette unité. Les élèves vont prendre conscience qu’on peut réaliser des polygones qui ont la même aire et pas nécessairement le même périmètre. Inversement, ils vont constater que certains polygones ont le même périmètre sans avoir nécessairement la même aire.
- En s’appuyant sur la trace des figures sur papier quadrillé, demander de reconstituer un carré, un triangle rectangle isocèle, un parallélogramme, un trapèze isocèle, un rectangle non carré avec les sept pièces du tangram (2) .
On peut demander aux élèves, à partir du carré et en déplaçant le moins de pièces possibles, de réaliser un triangle rectangle isocèle, puis un parallélogramme et enfin un trapèze isocèle. Faire remarquer que tous les polygones réalisés avec les 7 pièces ont la même aire.
(1) Jeux mathématiques, Akihiro Nozaki, Mitsumasa Anno, Éditeur Père Castor, Flammarion.
(2) Enseigner les mathématiques à l’école, F. Cerquetti-Aberkane, Hachette Education, Paris 2005.
Françoise Cerquetti-Aberkane, Marie-Christine Marilier