S’entraîner à utiliser les tables d’addition :
les cascades additives
CP-CE1-CE2-CM-6°
Objectifs :
S’entraîner à utiliser les tables d’addition en faisant du calcul mental.
Amener les élèves à calculer puis à réfléchir avec des nombres.
Consigne :
Remplir les cases de telle façon que chaque case contienne la somme des nombres situés en dessous.
Conseils :
Le professeur doit remplir la cascade, avant de la donner aux élèves. Le professeur explique la consigne collectivement puis circule dans les rangs dans la classe avec en main la solution.
Pour aider à comprendre la consigne, on peut commencer par une cascade dont la ligne du bas est la seule remplie. Par exemple on donnera aux élèves de CP ou de CE1 des cascades à 3 lignes avec des nombres entiers entre 0 et 10 en bas. (niveau grand débutant)
Exercices pour l'éléve
les solutions
Cascades niveau 1 (peuvent être utilisées pour comprendre la règle)
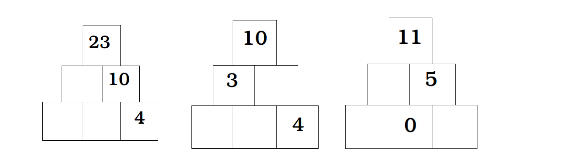
La 1° cascade a une seule solution, on peut la commencer en inscrivant 13 ou 6 indifféremment au milieu ou en bas. Une fois ces deux cases remplies, il reste à utiliser 7+6=13. On utilise des additions à trou qui sont équivalentes à une soustraction.
La 2° cascade est plus simple en commençant par 3+7=10. Si on la commence par le bas, il faudrait connaître (tâtonner avec ) les décompositions de 3 pour arriver à 3+4=7 puis 7+3=10. On commence à mettre en place la stratégie : par quelle ligne vaut-il mieux commencer ? Une seule solution.
La 3° cascade peut se commencer sur la 2° ligne ou bien sur la ligne du bas. Il n’y a plus ensuite à compléter en bas à gauche par 6. Une seule solution.
Cascades niveau 2
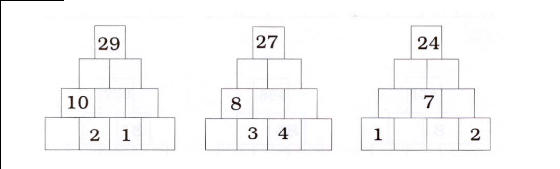
Les cascades ci-dessus sont plus difficiles car elles comportent une ligne de plus.
La 1° se remplit bien dans toute sa partie gauche en commençant par le bas (8 ; 2 ; 12). On continue par la droite en descendant (17 ; 15 ; 14). Une seule solution.
La 2° cascade, la stratégie est presque la même. Une seule solution. 5 en bas à gauche, puis 7 et 15 en montant. En descendant, 12, 5, 1.
La 3° cascade, nécessite de tâtonner avec les décompositions de 7 et/ou de 24. Il y a plusieurs solutions, c’est cela la grande nouveauté. En fait, toutes les décompositions de 7 sont utilisables. Avec certains élèves, il est possible de se demander pourquoi ?.
Cascades niveau 3
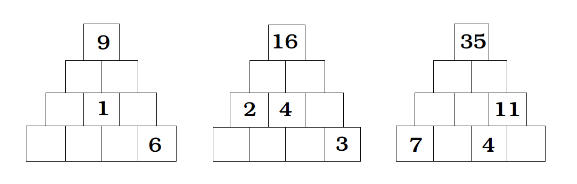
La première cascade a plusieurs solutions en fonction des décompositions de 1 que l’on inscrira sur le centre de la ligne du bas. On peut inscrire 0 ; 1 ou 1 ; 0. Cela permet dans ces deux cas de compléter la partie droite de la cascade de deux façons donc. Puis on remplit la partie gauche en commençant par le haut. Tout en bas à gauche, 3 solutions avec 0 ; 0 ou 1 ; 0 ou 0 ; 1. Toute proposition d’élève est à accepter, le professeur peut l’inviter à trouver d’autres solutions.
La deuxième cascade incite à commencer à inscrire 6 au-dessus de 2 et 4. Le reste devient très facile en continuant par la droite. Une seule solution.
En bas on trouve 1 ; 1 ; 3 ; 3. Elle serait niveau 2.
La dernière est très intéressante pour le tâtonnement et pour réfléchir aux calculs présents. On peut partir d’une réponse fausse pour la faire évoluer vers une réponse exacte. Par exemple, si on met au hasard sur la dernière ligne 7 ; 0 ; 4 ; 7 on obtient en haut 11 ; et 15 qui sont loin de faire 35 on obtient 26 l’écart pour aller à 35 est de 9.
Si je mets 7 ; 4 ; 4 ; 7 en bas j’obtiens en haut 19 ; 19 j’ai 3 de trop.
Un programme avec un générateur de pyramides additives permet de tâtonner mais on peut essayer de réfléchir pour trouver une bonne solution.
Une solution s’obtient avec 7 ; 3 ; 4 et 7.