Différentes façons de présenter un problème pour chercher :
Exemples de problèmes de dénombrement du type
« Combien de triangles ? de carrés ? de quadrilatères ?... »

1. Différentes façons de présenter un problème pour chercher.

On peut proposer un problème pour chercher de différentes façons. La consigne peut être uniquement orale, donnée oralement mais avec l'aide d'un écrit, uniquement écrite (support texte, ou schémas, tableaux, dessins), avec ou sans recours à un matériel. Un problème géométrique peut se présenter sous forme d’une figure, d’un solide ou même d'un assemblage à reproduire.

Voici un exemple de problème géométrique qu'on peut proposer au cours moyen. Il s'agit
de reproduire la figure ci-dessous :

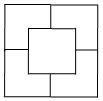
Dans un premier temps, on peut laisser émerger les procédures : beaucoup relèveront de l'approximation. Un calque mis à la disposition des élèves leur permet de contrôler qu'ils n'obtiennent pas une reproduction satisfaisante de la figure modèle.

On peut alors procéder à une première mise en commun, permettant la prise de conscience par les élèves qu'il faut analyser précisément la figure, trouver les relations entre les éléments qui la composent (alignements, milieux, ...).

Cette analyse peut alors être menée collectivement, à condition d'en laisser la responsabilité aux élèves, y compris si elle est incomplète ou partiellement erronée.

Nouvelle tentative des élèves, utilisant l'analyse précédente.

On organise ensuite une deuxième mise en commun, visant à valider ou invalider dessins et procédures. Il est alors intéressant de demander une validation qui soit de l'ordre de l'examen critique des procédures en elles-mêmes : a-t-on respecté les
éléments mise en évidence lors de l'analyse ? Est-on sûr, par exemple, que les milieux sont bien respectés ? ...

La validation pratique à l'aide du calque vient alors confirmer ce qui a été mis enévidence dans la phase précédente.

Un problème pour chercher peut également être proposé à partir d’un dispositif matériel. On peut, par exemple, proposer au CE1 un problème de partage de jetons en 3 ou 4 parts égales, en donnant, dans un premier temps, des boîtes et des jetons, pour aider à la représentation du problème. Dans un deuxième temps, les jetons sont dans une boîte fermée sur le bureau de l’enseignant : les élèves ne peuvent plus résoudre le problème avec le matériel. C’est la condition pour que les élèves soient confrontés à une résolution de type mathématique, et pas seulement à une manipulation.

2. Exemples de problèmes de dénombrement.

Cercles et droites, CM.

Ce problème est tiré du 5e Rallye Mathématique Transalpin.

« Dessinez deux cercles et trois droites, dont deux sont parallèles, de façon à obtenir le plus grand nombre possible de points d'intersection.
Combien obtenez-vous de points d'intersection au maximum ? ».

Ce problème relève de la catégorie des problèmes qui peuvent être résolus par essais et ajustements. On peut avoir aussi une part de déduction : si les 2 cercles se coupent, on aura plus de points d'intersection que s'ils ne se coupent pas. De même chaque droite doit couper chacun des deux cercles.

Par un tel raisonnement les élèves ont aussi accès à la preuve.

Les deux cercles se coupent au maximum en 2 points

Les deux parallèles coupent les deux cercles au maximum en 5 points chacune

La sécante aux deux parallèles coupe les deux cercles au maximum en 4 points et les deux parallèles en deux points.

Total 2+10+6=18

Partage de rectangle, CM.

« Comment partager un rectangle en 4 parties de même aire en traçant trois segments ? »

Ce problème est de ceux qui ne peuvent être résolus que par essais. L'un des intérêts de ce problème est qu'il comporte plusieurs types de solutions outre les solutions « évidentes », et que pour chacun des types il y a une infinité de solutions. En voici
quelques-unes :

Voici un problème du même type :

Comment partager un carré en 4 parties de même aire en traçant 2 segments ? en traçant 3 segments ?

Combien de carrés ?

Combien y a-t-il de carrés sur cette figure ?

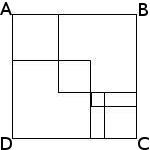
Il s'agit d'un problème de dénombrement qui relève de la catégorie « recherche de toutes les possibilités ».

La difficulté réside dans le fait d'être sûr que l'on a bien trouvé tous les cas.

La seule preuve est la production organisée de tous les quadrilatères ayant par exemple pour sommet, en haut et à gauche, successivement tous les points que l'on peut envisager sur cette figure, et qui sont des points d'intersection de deux côtés.

• Le carré ABCD
• De sommet A un carré autre que ABCD
• De sommet B un carré autre que ABCD
• De sommet C deux carrés autre que ABCD
• De sommet D un carré autre que ABCD
• À l’intérieur il y a deux carrés

En tout 8 carrés

Combien de triangles, de quadrilatères ?

Combien de triangles, de quadrilatères, sur ce dessin ?

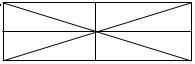
Il s'agit d'un problème de dénombrement, qui relève de la catégorie « recherche de toutes les possibilités ».

Seule l'organisation des essais permet d'être sûr d'avoir toutes les solutions.

Cordes CM.

Ce problème, tiré de Ermel CM2 (éditions Hatier), est de ceux qui amènent à la formulation d'une conjecture et à la production d'éléments de preuve.

Des points sont marqués sur un cercle. Il s'agit de trouver le nombre de cordes obtenues en joignant ces points deux à deux, et ceci quel que soit le nombre de points.

La recherche pour quelques exemples (pour 6 ou 10 points on peut dénombrer, puis ce n'est plus possible quand le nombre de points augmente) amène à formuler une règle générale, qui peut prendre deux formes.

Par exemple, pour 96 points, le nombre de cordes peut être obtenu, soit comme étant la somme des 95 premiers naturels à partir de 1 (1 + 2 + 3 + ... + 94 + 95), soit comme résultat de l'expression : (96 x 95) : 2.

Chacune de ces deux formes pour la solution peut être justifiée par un raisonnement produit par des élèves de CM.

Annie Peix, Professeur de Mathématiques
Marie-Christine Marilier (pour les réponses)