Mes élèves ont des difficultés à comprendre la technique de la multiplication :
la méthode « per gelosia » peut réconcilier les élèves
avec la technique opératoire classique.
On considère souvent que la technique de la multiplication est acquise en CM2 alors que
de nombreux élèves demeurent en difficulté, ne réussissant, que rarement, à calculer le
produit avec la technique classique. Or, rien n’impose la technique classique ; aussi il est
possible d’utiliser la suivante.
Présentation de la méthode :
Voici le produit de 165 par 72 calculé par la méthode « per gelosia » 1 , le produit se lit en
dessous, on obtient 11 880 :
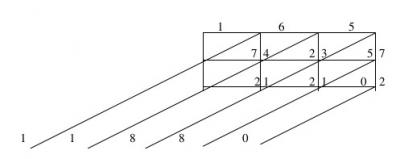
(Cette technique opératoire de la multiplication « Per gelosia » tire son nom des fenêtres à jalousies, sorte de
volets à travers lesquelles la lumière passe en diagonale et qui permettent de voir sans être vu.)
Pour trouver la réponse, on écrit le résultat des tables de multiplication dans chaque
rectangle :
Sur la première ligne : 1x7 ; 6x7 ; 5x7 ;
Sur la deuxième ligne : 1x2 ; 6x 2 ; 5x2 ;
Chaque rectangle est séparé en deux parties égales par une de ses diagonales. Le
produit de 165 par 72 s’obtient en ajoutant de droite à gauche, les nombres qui se
trouvent dans la même bande oblique.
Dans la bande de droite, il y a seulement 0. Ensuite, on ajoute 5+1+2 = 8 qui est placé
en dessous, etc.
Ici, sur l’avant dernière bande à gauche, la somme à effectuer comporte un résultat à
deux chiffres ; aussi, il y a une retenue à ne pas oublier et à reporter sur la diagonale
suivante.
Justification de la méthode :
Le résultat provient de la décomposition suivante, qui est en fait la somme des produits
suivants :
(1x7x1000) + (6x7x100) + (5x7x10) + (1x2x100) + (6x2x10) + (5x2)
chaque parenthèse correspondant à une case du quadrillage.
On remarquera qu’il y a bien 42 centaines (qui proviennent de 6x7x100= 4200) donc 2
centaines à ajouter à 2 centaines qui proviennent de 1x2 et 1 centaine qui provient de
6x2x10=120. La disposition en diagonale les met sans effort ensemble et il suffit alors de
les ajouter. Cette justification mathématique permet de comprendre comment la
disposition pratique met les bons nombres en correspondance. Il n’est pas obligatoire de
le communiquer aux élèves.
Aspects pédagogiques :
Cette technique ne vise pas à remplacer la technique classique (même si elle peut le
faire) mais vient plutôt en complément. Elle constitue une autre approche de la
multiplication qui permet aussi d’éclairer la technique classique. Elle peut également
permettre de vérifier un résultat obtenu par toute autre méthode. Il est ainsi important
de laisser aux élèves, le plus souvent possible, le choix de poser la multiplication comme
ils le souhaitent et d’utiliser la technique de leur choix.
Elle présente les avantages suivants :
Pour les élèves :
Elle est plus simple que la technique classique, car chaque case correspond au résultat
d’une table de multiplication, sans autre calcul. Le professeur peut même décider de
donner les tables (à l’aide d’un document papier ou un affichage collectif), à un élève en
grande difficulté ou l’autoriser à s’aider des doigts. L’élève peut également se relire et
vérifier après coup si ses tables sont connues. Ensuite, il n’a pas à gérer les
multiplications et les retenues issues des additions en même temps. Ces calculs sont bien
séparés. Le calcul peut être interrompu sans gêne, les élèves distraits ne sont pas
handicapés. Le décalage de ligne n’apparaît pas. Les élèves peuvent donc être facilement
en situation de réussite, reprendre confiance, et évidemment utiliser le résultat dans un
problème.
Pour le professeur :
Les erreurs dans les tables de multiplication sont faciles à détecter et le professeur peut
percevoir celles qui sont à retravailler. La correction permet de distinguer l’erreur de
retenue dans l’addition des erreurs de calcul mental dans les multiplications. Son seul
inconvénient est une certaine lourdeur de mise en oeuvre car il faut dessiner un tableau.
Aussi, il est vivement conseillé de proposer aux élèves des tableaux non remplis que le
professeur aura pris soin de photocopier. Il faut également faire des cases suffisamment
grandes pour que la disposition des chiffres en bandes obliques ne soit pas trop confuse
et que les additions soient clairement faites en oblique. L’année de CM2 est une année
importante et décisive pour arriver à aider les élèves sans que cela prenne trop de
temps. Cette technique le permet. Elle peut être également utilisée en aide individualisée
en classe de sixième.
Marie-Christine Marilier (2009)