Partie 1 Aspects didactiques

La proportionnalité est un objectif d’apprentissage du collège. A l’école primaire l’enseignant ne fait qu’une initiation à la proportionnalité, à partir
des tableaux de nombres et de lecture de graphiques. Les applications abordées restent simples, ainsi les pourcentages utilisés sont des
pourcentages en liaison avec les fractions simples.
En didactique, comme dans les programmes, on distingue différents contextes qu’on appelle cadres ou registres. On distingue les cadres
numérique, graphique, géométrique et algébrique.
Le cadre numérique correspond à l’utilisation de la proportionnalité avec des nombres essentiellement. Les procédures de résolution de problèmes sont numériques.
Le cadre graphique, comme son nom l’indique, exprime la proportionnalité à l’aide de représentation graphique dans le plan muni d’un repère. Les procédures utilisées concernent les points dans un repère.
Le cadre géométrique utilise les figures géométriques. Le théorème de Thalès est une application de la proportionnalité dans le cadre géométrique. Les méthodes de résolution de problèmes utilisent les points, les segments, les droites.
Le cadre algébrique utilise les lettres, les égalités et les fonctions, fonctions linéaires ou pas !

A l’école primaire, bien évidemment le cadre algébrique ou le cadre fonctionnel ne sont pas utilisés.

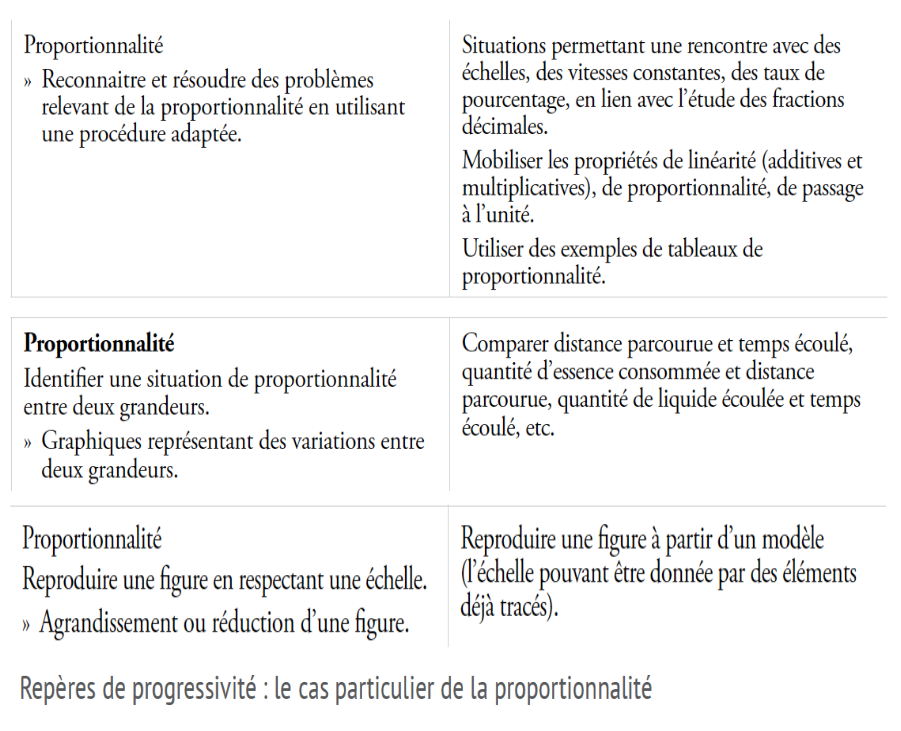
Voici un extrait des programmes de CM1, CM2 et de sixième :

Partie 2 Aspects mathématiques

Définition : (cadre numérique)
On dit que deux suites de réels ayant le même nombre de termes sont proportionnelles quand on peut obtenir chaque terme de la deuxième suite en multipliant les termes de la première par un nombre réel appelé coefficient de proportionnalité noté ici a.
La deuxième suite est appelée image de la première.

Exemples :
Exemple 1 : Sur la première ligne du tableau qui suit, est indiqué le nombre de places de théâtre.
Sur la deuxième ligne le prix total à payer

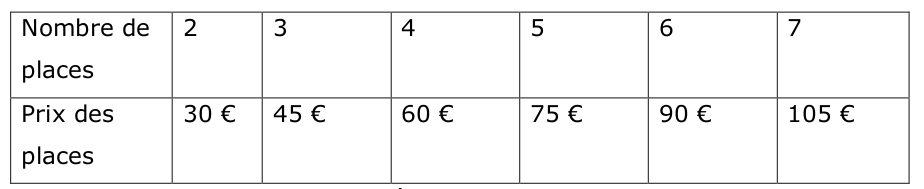
Le coefficient de proportionnalité est 15.
On écrit a=15, ici c’est un nombre entier.

Exemple 2 :

Le coefficient est un nombre décimal qui s’écrit soit 0,75 ou 3⁄4.
Remarque 1 : Si on inverse l’ordre des lignes, on a encore une situation de proportionnalité mais dans le deuxième tableau le coefficient est alors 4/3 au lieu de 3⁄4.
Remarque 2 : Un tableau de proportionnalité peut se présenter également en colonnes, il y a alors proportionnalité entre les colonnes.

Remarque 3 : Il faut que les deux suites comportent au moins deux termes. Un tableau de proportionnalité peut prendre la forme de 4 cases.

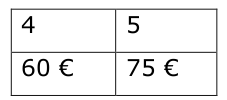
est un tableau de proportionnalité.
Remarque 4 : Les nombres présents dans le tableau ne sont pas ordonnés toujours du plus petit au plus grand.
Remarque 5 : Il est tout aussi important de reconnaître un tableau de proportionnalité qu’un tableau de non-proprotionnalité.

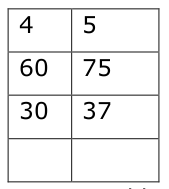
n’est pas un tableau de proportionnalité, il aurait fallu mettre 37,5.

Propriétés des tableaux de proportionnalité
1) Dans un tableau de proportionnalité, le nombre qui correspond à 0 est 0. En effet, 0xa=0.

2) Propriété de linéarité additive

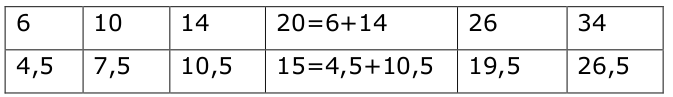
On remarque que 20=6+14 et que les images correspondantes 4,5 et 10,5 s’ajoutent pour donner l’image de 20.
L’image d’une somme est la somme des images, c’est la linéarité additive. On écrit :
                      f(6)+f(14)=f(20) ou f(6)+f(14)=f(6+14)
Cette propriété est vraie pour toutes les valeurs du tableau.

3) Propriété de linéarité multiplicative

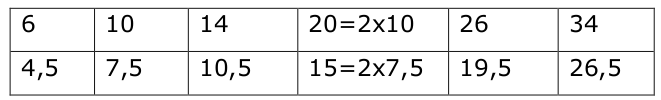
L’image du double de 10 est le double de l’image de 10.
On écrit f(2x10)=2xf(10)
Cette propriété est vraie pour toutes les valeurs du tableau.

Procédures de calcul, des rapports égaux
Pour trouver le coefficient de proportionnalité, on écrit les quotients obtenus en divisant les nombres de la 2° ligne par ceux de la première.

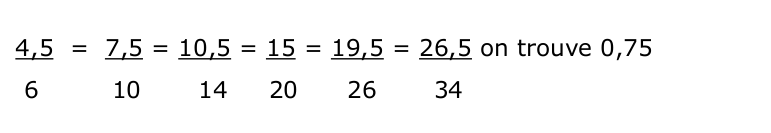
Le retour à l’unité
Il s’agit de chercher le nombre qui correspond à l’image de 1.
Ici, 1 a pour image 0,75. 1 a toujours pour image a, le coefficient de proportionnalité.

Propriété des produits en croix :
Deux quotients a/b et a’/b’ sont égaux si et seulement si axb’=a’xb
Cette propriété est très utile pour chercher une valeur dans le tableau.

La propriété des écarts
On remarque dans le tableau ci-dessus que sur la première ligne entre 6 et 10, entre 10 et 14, les écarts sont identiques et égaux à 4. Les valeurs correspondantes sur la deuxième sont entre 7,5 et 4,5 de 3, et il en est de même entre 10,5 et 7,5. Ceci se note
f(14-10)=f(14) - f(10) ou f(14-10)=f(14) - f(10)
Cette propriété est vraie quels que soient les nombres d’une situation de proportionnalité.

La règle de trois
Il s’agit d’un raisonnement qui fait intervenir 3 nombres.
Reprenons l’exemple des places de théâtre et cherchons le prix de 14 places, on peut dire que si 2 places coûtent 30 euros, 1 place coûte 15 euros et 14 places coûtent :

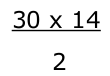
C’est à dire 420 : 2 = 210 euros on effectue le calcul comme on veut indépendamment du sens ci-dessus.

Représentation graphique
Dans un repère Oxy, dans le cas d’une situation de proportionnalité on obtient une succession de points alignés sur une droite avec l’origine du repère O.

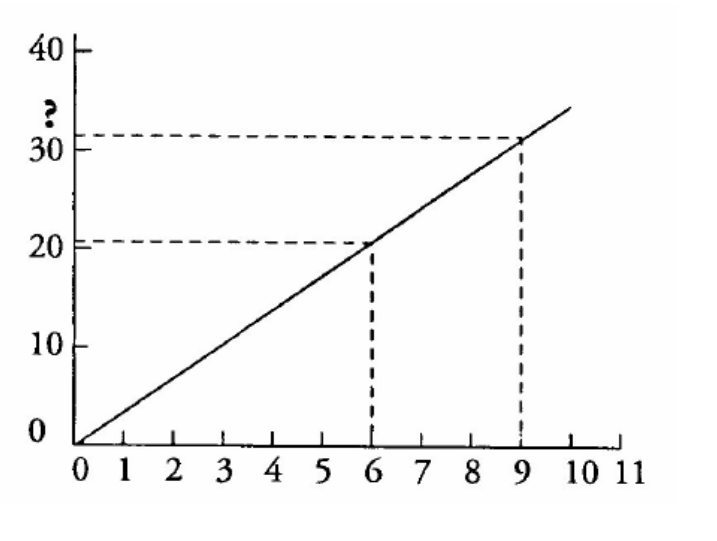
Sur le graphique ci-dessus les suites (6 ; 9) et (21 ; 31,5) sont proportionnelles en effet, 6x31,5= 189 et 21x9=189. Les points A(6,21) et B (9 ; 31,5) sont alignés avec O. Une situation n’est pas une situation de proportionnalité soit parce que les points ne sont pas alignés, soit parce qu’ils sont alignés mais pas avec l’origine.