Correction des exercices de la feuille sur la division euclidienne

Exercice 1:
Technique opératoire de la division 738 divisé par 12.

738  = 12 x ? + ?

En appliquant un algorithme il faut trouver la valeur des deux points d’interrogation.

• 1° méthode :

On fait une liste des multiples de 12 jusqu’à approcher 738 au plus près. 12 x 50 = 600 ; 12 x 60 = 720 on approche ; 12 x 61 = 732 c’est bon ! 738 = 12 x 61 + 6 le quotient est 61 et le reste 6.

• 2° méthode :
  

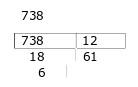
73 dizaines partagées en 12 parts égales donne 6, il reste 1.

18 unités partagées en 12 donne 1 unité et il reste 6 unités.

 

Exercice 2 :

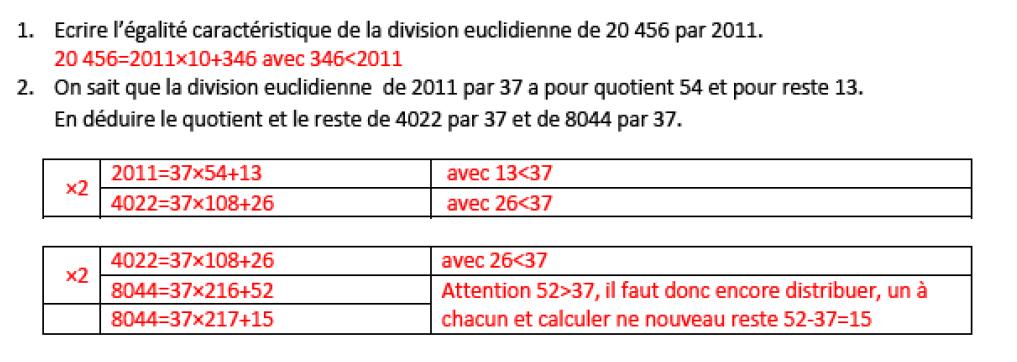
Exercice 3 CRPE

Le rangement des nombres obtenus dans le tableau rectangulaire est organisé en 7 colonnes.

 

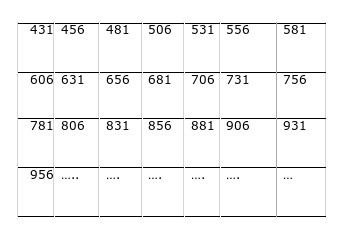
1) Dans le tableau les nombres vont de 25 en 25, comme 4x25=100, au bout de 4 cases, on trouve une centaine de plus. Toutes les 4 cases, le nombre se termine donc par 31, ajouter 100 ne modifie que le chiffre des centaines.

2) Pour que les nombres ayant le même chiffre des unités et même chiffre des dizaines se situent tous dans la même colonne il faudrait 4 colonnes, en effet c’est le 5° nombre qui égal au premier nombre plus 100.
 

3) Tous les nombres de la première colonne du tableau donné ci-dessus et rien qu’eux s’obtiennent en ajoutant 175 c'est-à-dire 7x25. ON obtient tous les nombres de la première colonne en comptant de 175 en 175 à partir de 431.

4) Le nombre 1131 a sa place dans ce tableau : il a 200 de plus que 931 donc 8 cases plus loin. 5° ligne, 1° colonne. C’est 956 + 175 = 1131. Quant à 8626=431+8195, comme 8195 n’est pas un multiple de 25, il n’a pas sa place dans le tableau.
 

5) Le nombre qui se situe à la 20° ligne et à la 5° colonne de ce tableau est 431+19x175+4x25=3856.
 

6) Un nombre compris entre 5600 et 6000 qui a sa place dans la 3° colonne, on le cherche sous la forme :

431+ ? x 175+ 2 x 25 = 481+ ? x 175

Sur la 30° ligne on obtient 481+ 29 x 175=5556
Sur la 31°ligne on obtient :481+ 30 x 175=5731
Sur la 32°ligne on obtient: 481+31x175=5906
Sur la 33° ligne on obtient: 481+32x175=6081
Il y a deux solutions.
 

7) Sur une page, on met 50 lignes. Combien de pages sont nécessaires pour prolonger ce tableau jusqu’à ce qu’au moins un nombre supérieur à un million apparaisse ?

Sur la 1° page, 1° colonne on arrive à 431+175x49=9006 Sur la n° page à 431 + 175 x 49 + 175 x 50(n-1) >1 000 000 Sur la page 115, on obtient :

431 + 175 x 49 + 175 x 50 x 114 = 1 006 506

On peut faire 1 000 000 – 431 – 175 x 49 = 990994

Diviser par 175x50=8750 donne 113 avec un reste égal à 2244 La réponse est donc page 113.

8)

n vaut 37.

13258-13036 = 6 x 37 = 222. Il y a donc 6 colonnes.
 

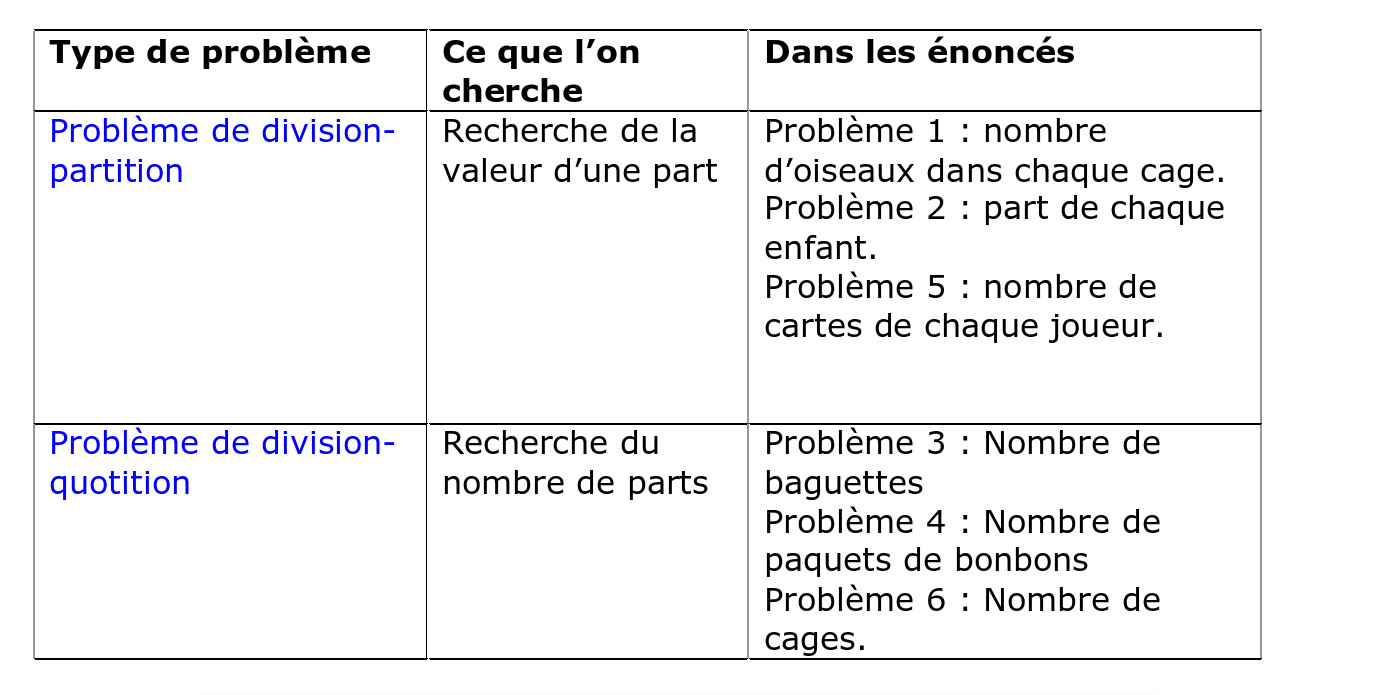
Exercice 4

Ce sont tous des problèmes de partages en parts égales, ce qui les partage en deux catégories c’est le but de la question, c’est ce que l’on cherche.

Exercice 5 : (CRPE Bordeaux)

On cherche un nombre entier n tel que n = 25 x q + r avec r<25 et q = r.

donc n = 25 q + q = 25 q + 1 q = 26 q

n est donc un multiple de 26.

Les multiples de 26 sont 26 ; 52 ; 78 ; 104 etc …. Il y a une infinité de

solutions.

 

Exercice 6 :

On cherche a et b tels que a = b x 82 + 47. avec a < 3 000 et dans toute division le reste est inférieur au diviseur.

47 < b ;

On peut donc prendre pour b des valeurs à partir de 48 et calculer la valeur de a correspondante.

b x 82 + 47 < 3000 ! b < 2953 : 82 ! b < 36 , 01

Il n’existe aucune valeur de b inférieur à 36 et supérieur à 47.

Ce problème n’a pas de solution.

 

Exercice 7 :
Peut-on déterminer les entiers naturels de 2 chiffres qui, divisé par 37, donnent un quotient égal au reste ? Justifier.

On procède comme dans l’exercice 4.

a = 37 q + r , a est un multiple de 38.

Les multiples de 38 possibles sont 38 ; 76 .

 

Exercice 8 CRPE
(dans cet exercice, il n’est pas souhaitable de poser les divisions, mais il vaut mieux utiliser les égalités pour s’entraîner à utiliser la définition de la division euclidienne et d’utiliser les propriétés des égalités. Néanmoins, la division posée peut donner la réponse ou permettre de vérifier)

1) On décompte de 3 en 3 à partir de 50 tant qu’on obtient un entier naturel : 50, 47, 44, 41, 38, 35, 32, 29, 26, 23, 20, 17, 14, 11, 8, 5, 2. Cette liste est tout à fait satisfaisante et permet de trouver les résultats à coup sûr. Le dernier terme est 2.

En effet, on peut aussi pour aller plus vite, écrire 50-3x16=50-48=2. Cette suite a 17 termes.
Remarque : Le dernier terme de la suite est le reste de la division euclidienne de 50 par 3.
 

2) On décompte de 3 en 3 à partir de 8932 tant qu’on obtient un entier naturel : 8932, 8929, 8926, 8923 ….Pour aller plus vite on enlève des « paquets » de 3, 8932-6000=8932-3x2000=2932, puis 2932-3x900=232 puis 232-3x70=22 puis encore 22-3x7=1.

Le nombre qui termine cette suite est 1.

Le dernier terme de la suite est le reste de la division euclidienne de 8932 par 3.

Le nombre de termes est : 1+2977=2978. Le 100° terme est 8932-99x3=8932-297=8635.
 

3) Sachant que 8562 = (34 x 251) + 28 en lisant directement cette égalité.

Le quotient est 251 et le reste est 28 de la division euclidienne de 8562 par 34. Le reste 28 est bien inférieur au quotient 34.

Le quotient est 34 et le reste est 28. On peut vérifier en posant la division.
 

4) Sachant que 1 261 541 = (4897x257) + 3012 ; en multipliant par

100 chaque terme, on obtient :

126 154 100 = (489 700 x 257) + 301200.

Le quotient est 257 et le reste est 301200 dans la division euclidienne de 126 154 100 par 489 700.
 

Exercice 9

1) La division euclidienne de n par 3 s’écrit n=3q+r avec r<3 ici r=1. Donc n=3q+1 (le reste est inférieur au diviseur)

Le prédécesseur est n-1=3q+1-1 donc n-1=3q, le reste est 0, on a 3q+0 ;

Le successeur n+1=3q+1+1=3q+2. Le reste est 2.
 

2) La somme de 3 entiers consécutifs s’écrit :  n+(n+1)+(n+2)  = 3n+3=3(n+1) c’est un multiple car le résultat de multiplication par 3. On dit aussi que le résultat (la somme) est divisible par 3.
 

3) La somme des carrés s’écrit :
n2 + (n+1)2+ (n+2)2 = n2+ (n2+2n+1) + (n2+4n+1)=3n2+6n+2 = 3(n2+2n) +2 qui n’est pas un multiple de 3 car le reste est égal à 2.

Exercice 10

1)
On a :
57 148 468 = 3 361 674x17 + 10 et

84 279 733 = 4 957 630x17 + 23

On en déduit que :

57 148 468 + 58 279 733= 3 361 674x17 + 10 + 4 957 630x17+23
57 148 468 + 58 279 733= 3 361 674x17 + 4 957 630x17+10 + 23
57 148 468 + 58 279 733= (3 361 674+ 4 957 630)x17+33
LE RESTE N’EST PAS 33 CAR 33 N’EST PAS INFERIEUR A 17.

IL FAUT CASSER 33 en 17+16 et faire rentrer un 17 dans le quotient.

Le quotient est donc 3 361 674+ 4 957 630+1=

Le reste est 16.

Enfin on sait que :
58 148 468 = 3 361 674x17 + 10
59 148 468x2 = 3 361 674x17x2 + 10x2

Le quotient n’est pas 3 361 674x2 et le reste n’est pas 20 (il y en a qui sont aller trop vite !!)

Il faut casser 20 en 17+3 et donner un 17 avec le premier produit 148 468x2 = 3 361 674x17x2 + 17+3=(3 361 674x2+1)x17+3

Le quotient est donc 3 361 674x2+1=6 723 349

Le reste est 3.

2)
a=17q+r avec r<17 et a’=17q’+r’ avec r’<17.
LE QUOTIENT de a+a’ par 17 N’EST PAS toujours q+q’ (vous êtes allés trop vite et oui !) a+a’=17(q+q’)+r+r’ en effet mais r+r’<17+17 donc r+r’ peut être inférieur à 17 ou compris entre 17 et 34. La condition sur le rest est essentielle.

Il y a donc 2 cas :

• Si r+r’<17 alors le quotient est q+q’ et le reste est r+r’
• Si 17=<r+r’<34 alors le quotient est q+q’+1 et le reste est r+r’-17
   

Pour 2a c’est la même chose, 2a=2(17q+r)=34q+2r avec r<17

Le quotient n’est pas toujours 2q si vous avez répondu cela, vous êtes passé à côté de la condition sur le reste et il faut aller plus en réfléchissant…

Il y a encore 2 cas, car 2r<34 ; il faut distinguer 2r<17 et 17=<r<34

• Si 2r<17 alors le quotient de 2a par 17 est 2q et le reste est bien 2r
• Si 17=<2r<34 alors le quotient est 2q+1 et le reste r+r’-17.