Si vous avez besoin de conseils. Contactez-moi.

Exercice 1
• Procédure 1 : déterminer d’abord le montant de l’augmentation
La question peut se traduire ainsi :

Toutes les procédures de relatives aux problèmes de recherche d’un quatrième proportionnelle sont possibles, comme par exemple :

-Utiliser la linéarité : on passe de 100 à 1595 en multipliant par 15,95, l’augmentation est donc de 7×15,95€, soit 111,65€ ;

-Utiliser le coefficient de proportionnalité entre les grandeurs « prix initial » et « augmentation » : c’est 7/100. Appliqué à 1595, cela va donner :
1595×7/100=111,65€.
Le prix après augmentation est donc de 1595+111,65=1706,65€.
Pour calculer 7% d’une quantité, on peut revenir à la proportionnalité ou se souvenir du fait que prendre 7% revient à multiplier par 7/100.

• Procédure 2 : déterminer directement le prix après augmentation
Augmenter de 7%, c’est multiplier par 1+7/100, c’est-à-dire par 1,07. Le
prix après augmentation est donc donné par :
1595×1,07=1706,65€.

Exercice 2

1. On demande la vitesse moyenne connaissant la distance et la durée du parcours.
La vitesse moyenne du coureur est donnée par v=dt=508=6,25m/s

Réponse : 6,25 m/s.

2. On demande la distance connaissant la vitesse moyenne et la durée du parcours.

Commençons par exprimer 1h55min en heures :

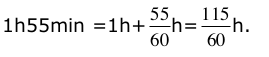
La distance Paris-Lyon est égale à : d=v×t=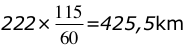  

3. On demande la durée du parcours € connaissant la vitesse moyenne
et la distance.
Pendant la première partie
il a parcouru : 120km (v×t=80×1,5=120), et,
pendant la deuxième : 150km en effet, v×t=100×1,5=150).
Soit 270km en 3h, donc une vitesse moyenne de 90km/h
(v = d : t = 270 : 3 = 90).
Exercice 3

Exercice 4

-Dans une échelle de « 2cm pour 5m », 5m dans la réalité sont représentés par 2cm.
Dans une échelle de 1/25000, 25000cm sont représentés par 1cm.
1/25000 représente le coefficient de proportionnalité entre les dimensions réelles et les dimensions représentées. Dans ce cas les unités des
dimensions doivent être les mêmes. Les problèmes d’échelle se traitent donc en utilisant les procédures habituellement utilisées pour les situations qui relèvent de la proportionnalité

Exercice 5
Les propositions suivantes sont-elles vraies ?
1) Augmenter de 30%, c’est multiplier par 1,30. VRAI
2) Diminuer de 25%, c’est multiplier par 0,70.
3FAUX, c’est 0,75.
3) Deux augmentations successives de 12% et de 27% correspondent à une augmentation de 39%.
FAUX
on multiplie par 1,12 x 1,27=1,4224 ;
l’augmentation est de 42,24%.
4) Un litre de limonade contient 80% d’eau, donc un demi-litre de limonade contient 40% d’eau.
FAUX, il en contient aussi 80%, la proportion d’eau est la même.

Exercice 6
1° Le prix augmenté de l’article doit diminuer de 20% pour revenir à son
prix initial.
On aurait pu utiliser un schéma sachant de 25% représente le quart du
prix initial de l’article :

Exercice 9
Réponse : Si x est le prix de l’article au départ, après la première démarque le prix est multiplié par 0,60 après la deuxième démarque le
prix est multiplié par 0,90 puis enfin par 0,80. finalement le prix de départ est multiplié par 0,6x0,9x0,8=0,432.
Le pourcentage de réduction au total est donc de 100-43,2=56,8%.

Exercice 10
La nouvelle longueur est : Lx0,80
La nouvelle largeur est lx0,80
Le nouveau périmètre est diminué de 20% aussi.
La nouvelle aire est de Lxlx0,80x0,80=Lxlx0,64
L’aire diminue de 36%.