Exercice 1
Le nombre de départ est 20, le nombre final est toujours le triple du nombre de départ. En effet, si j’appelle x le nombre de départ le programme de
calcul se traduit par :
(x-2) x 3+6
qui est égal à 3x
Exercice 2
E = 2x-1
E=0 a pour solution x=1/2.
Exercice 3
Si on appelle n le nombre du milieu on cherche n tel que (n-1)n(n+1) = 3n ;
soit n(n-1 ) = 3n d’ou (n-1 ) = 3 et n= 4 et n=2 donc les 3 nombres sont : 1, 2, et 3.
Exercice 4
Si on note x la largeur du champ, alors la longueur vaut 4x, et la surface vaut alors x * 4x = 4x², et celle du champ carré vaut 40² = 1600. Donc 4x² = 1600, et x² = 400. Donc x = √400 ou -√400. Or ici il s'agit d'une longueur, donc elle est positive, donc x = √400 = 20. les dimensions du champ sont donc 20m sur 80m.
Exercice 5
Si on appelle l et L la largeur et la longueur de mon salon, alors l*L = 49 et 2l + 2L = 28. On peut transformer la deuxième équation en la divisant par 2, ce qui donne l + L = 14, et on peut écrire l = 14 - L, ce qui nous donne en remplaçant l par 14 - L dans la première équation, (14 - L)*L = 49, ce qui, en développant, nous donne 14L - L² = 49, ou encore 0 = 49 - 14L + L². il faut reconnaître ici la première identité remarquable pour factoriser. Cela donne : (7 - L)² = 0, et donc L = 7.
Mon salon a pour dimensions 7m sur 7m (c'est donc un carré)
Exercice 6 : CRPE
1) a. A=(x+1)(x−1) − (x+2)(x−2)
On peut développer soit avec la double distributivité soit avec une identité remarquable. On obtient :
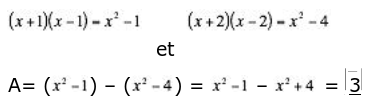
b. 297 × 295 − 298 × 294 ; ce calcul peut s’écrire :
(296+1)(296-1) – (296+2)(296-2)
C’est un cas particulier du calcul littéral de la question précédente, x vaut 196. Sans calcul, on peut affirmer que le résultat est 3 puisque c’est un cas particulier A.
2) a et b étant consécutifs on peut écrire que b = a+1, la somme de a et de b est égale à 2a+1.
Le carré de leur différence est égale à 1, la différence de leurs carrés est égale à : b-a= (a+1)-a= 2a+1.
C’est la proposition 1- qui est vraie.
Exercice 7 :
A) Solution arithmétique : l’écart entre l’âge du père et celui du fils est de 32 ans. Cet écart ne changera jamais.
<------! âge du fils
<------!<----------32 ans---------! âge du père
L’âge du père est le double du fils quand le fils aura 32 ans ! Le père aura alors 64 ans.
Solution algébrique : si on appelle x l’âge du fils
Pour que l’âge du père soit le double de celui du fils,
il faut que (x+32)=2x ; on trouve x = 32.
B) Dans un an, Laure aura le tiers de l'âge de Sam, alors qu'il y a un an, Laure n'avait que le quart de l'âge de Sam. Calculer l'âge de Laure.
Réponse : Appelons x l’âge de Laure, aujourd’hui.
Dans un an l’âge de Laure sera x+1 l’âge de Sam sera 3(x+1),
il y a un an, l’âge de Laure était x-1 et l’âge de Sam 4 (x-1).
L’écart entre 3(x+1) et 4(x-1) est de 2 ans, on peut écrire :
3(x+1)=4(x-1)+2 d’ou 3x+3=4x-4+2
c’est à dire 3+4-2=4x-3x donc x=6 ans.
Exercice 8 CRPE 2018
1. Dans 45, il y a 4 dizaines, 4x5=20 ce qui donne le nombre de centaines,
On écrit 25 à la droite du nombre obtenu, on obtient 2025.
2. le carré de n s’écrit :
(10d+5)(10d+5)=10dx10d + 10dx5 + 10dx5 + 5x5
= 100d + 50 d + 50d + 25 = 100d + 100 d + 25 = 100d(d+1)+25.
3. d(d+1) est le produit de l’étape 1, multiplié par 100, indique le nombre de centaines, si on ajoute 25, cela revient à juxtaposer 25.
4. 3,5 = 3+0,1x5 = 35x0,1
On peut calculer le carré de 35 et le diviser par 100.
3x4=12, le carré de 35 est donc 1225 et le carré de 3,5 est 12,25.
Exercice 9
Soit x le nombre de pièces de 10 centimes, et y le nombre de pièces de 20 centimes. `
Si on traduit les données de l'énoncé à l'aide de x et de y, cela donne :
x + y = 40
0,10 x + 0,20 y = 4,20
Si on procède par substitution, on a y=40-x si on remplace dans la deuxième équation, on obtient :
0,10x+0,20(40-x)= 4,20 d’où, 0,1x-0,2x+8=4,2 on trouve x = 38 et Y=2.
Exercice 10 CRPE 2018
Faux, l’inverse de la somme de 2 et 3 est 1/5. L’inverse de 2 est ½, l’inverse de 3 est 1/3 et ½+1/3=5/6.