Exercice 1 (CRPE 2018 groupement 3)
1) On peut présenter les données dans un tableau de nombres :

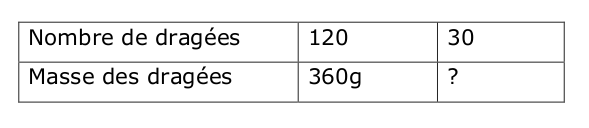
Il s’agit d’un calcul de quatrième proportionnelle.

Les élèves de CM2 peuvent utiliser les procédures suivantes qui sont dans les programmes officiels :

-le retour à l’unité :
L’élève peut d’abord se ramener à la masse d’une dragée qui s’obtient en divisant 360g par 120 soit 3g pour une dragée. La masse de 30 dragées est le produit de la masse d’une dragée 3g par 30. On obtient 3x30=90g.

-la règle de trois
On rassemble le raisonnement précédent, le raisonnement est le même mais ce qui diffère c’est que l’on ne calcule pas la masse d’une dragée, on pose le calcul qui s’écrit :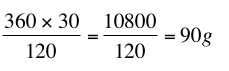                 

la façon de calculer est laissée libre. Par exemple ici, j’ai calculé le numérateur d’abord mais j’aurais pu faire la calcul

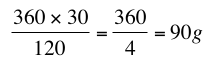
La différence entre la règle de trois et le retour à l’unité n’est pas dans le raisonnement mais dans la façon de mener le calcul.

-la linéarité multiplicative
Dans ce tableau, la linéarité multiplicative s’applique entre les colonnes. Il est clair que le nombre de dragées est quatre fois plus petit donc les masses sont dans le même rapport de 1⁄4. La masse est donc de 360 :4 = 90 g.

-le coefficient de proportionnalité
Le coefficient de proportionnalité 3 concerne les lignes entre elles. Pour passer de la première ligne à la deuxième, il faut multiplier par 3.

En effet, 120 x 3 = 360, il faut multiplier par 3 le nombre 30 pour obtenir la masse des 30 dragées. On obtient 90g.

L’égalité des produits en produits en croix n’est pas dans les programmes de CM2.

2) Pour encourager vivement le retour à l’unité, il faudrait décourager les élèves d’utiliser les autres procédures et donc que le coefficient multiplicateur et le coefficient de proportionnalité.
En posant le problème suivant :
120 dragées pèsent 300g, combien pèsent 50 dragées ?

Le coefficient de linéarité multiplicative est 50 : 120 = 5 : 12 = 0,
416666 .... qui est rationnel non décimal et le coefficient de proportionnalité qui est égal à 300 : 120 = 30 : 12 = 2,5 qui est un nombre décimal, ces nombres ne sont pas des nombres entiers donc difficiles à trouver pour des élèves de CM2.
La procédure de la règle de trois est néanmoins toujours possible à utiliser et accessible à des élèves de cycle 3 :

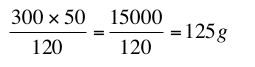
Exercice 2
1) Pendant huit secondes, c’est la partie de la courbe parallèle à l’axe des abscisses.
2) Le parachute s’ouvre quand la vitesse n’augmente plus, c’est en chute libre que la vitesse augmente. C’est donc au bout de 3 secondes.
3) La vitesse décroit de 25 m/s à 5 m/s.
4) Entre 6 et 14 secondes, le parachutiste est à la vitesse de 5m/s. Il parcourt donc 5m par seconde pendant 8 secondes. Il parcourt donc une distance de 5x8=40 mètres.

Exercice 3
- Faux, on peut travailler deux fois plus et que la note ne soit pas deux fois plus grande.
- Vrai, si toutes les pommes sont identiques (ce qui est très difficile, je vous le concède). Le coefficient de proportionnalité est la masse d’une pomme. J’accepte que vous répondiez que la phrase est fausse si vous argumentez.
- Vrai, dans tous les cas, à moins qu’il y ait des soldes, ou des pommes cadeaux.
- Vrai si la vitesse est constante, faux autrement. d=vt le coefficient de proportionnalité est la vitesse.
- Faux, car le prix x devient x-15. Nous n’avons pas y=ax.
- Vrai, le prix est multiplié par 0,85.
- Vrai, la formule pour le périmètre du cercle est p=2 Π R
- Faux, la formule pour l’aire du disque est égale à Π R 2

Exercice 4
1-Le thème mathématique de cette situation est la proportionnalité.
2-La procédure correcte à utiliser est une procédure telle que les anciennes dimensions et les nouvelles sont proportionnelles. Ceci est indispensable pour que les pièces du puzzle agrandies puissent s’assembler.

Pour remplir ce tableau, on peut utiliser le coefficient de proportionnalité 1,5 mais il est difficile à trouver pour des élèves de cours moyen, dans les programmes cependant.
On peut utiliser la linéarité multiplicative pour trouver 3 dans la première colonne puis 9 avec la linéarité additive combiné avec le retour à l’unité.
3-Cette situation est une situation d’apprentissage intéressante pour au moins 3 raisons :

-le contenu mathématique avec une présentation géométrique qui prend à la fois une forme un peu ludique et qui est un problème numérique qui fait réfléchir. Les élèves doivent trouver une procédure numérique pour agrandir toutes les pièces du puzzle afin d’obtenir un nouveau puzzle plus grand.

-le travail en petits en groupes permet de mettre en place une collaboration basée sur l’entraide, basée sur la communication entre pairs. Elle est facilitée par une production commune sous forme d’affiche.

-la possibilité de tester si la procédure est correcte avec vérification en reconstituant le puzzle.

4-Utilisation de l’addition (+2) sur deux côtés du carré (à droite et en bas) ; Addition avec +3 pour d’autres côtés par exemple.
L’addition n’est pas celles qui permet de répondre à la question mais qui est le plus utilisé par les élèves parce qu’elle représente eux davantage une augmentation, un agrandissement..

Exercice 5

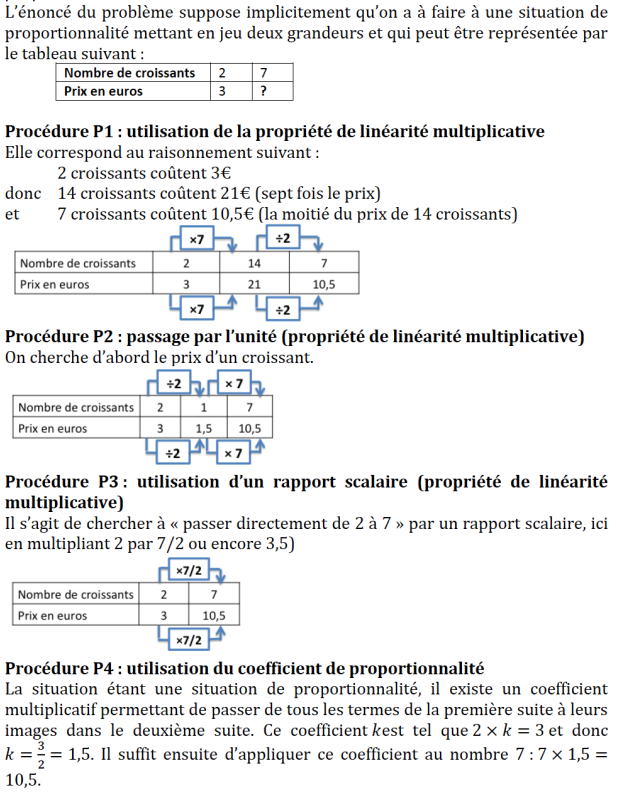
Exercice 7
1) Il est conseillé d’utiliser les points indiqués par les pointillés, ce sont les plus précis et les plus facile à lire.

Pour V1, on obtient la consommation aux 100 km en doublant la distance, on obtient 6l.
Pour V2, même raisonnement, on obtient 8l aux 100km.
Pour V3, on multiplie par 4, on obtient 12l aux 100km.
Pour V4, on multiplie par 2,5 en effet, 100=40x2+20, on obtient 6x2,5=15 l aux 100km.

2) Par lecture graphique, on cherche pour 1 litre en ordonnée, qui est obtenu pour 1cm, l’abscisse correspondante :
1,6 cm donne la consommation pour V1, il reste à chercher le nombre de kilomètres représentés par 1,6cm. Comme 25km sont représentés par
2,5cm, 1,6cm représentent 16km.
On reprendra ce raisonnement pour tous les véhicules.
V1 16km, V2 12 km, V3 8km, V4 6km.

Exercice 8
1) Tarif 1 : 7,5x6=45€ ; Tarif 2 : 6x6+18=54€ ; le tarif 1 est plus avantageux.
2) Méthode 1 : Le tâtonnement (très utilisé en général) présenté dans ce tableau en faisant la liste exhaustive des prix.

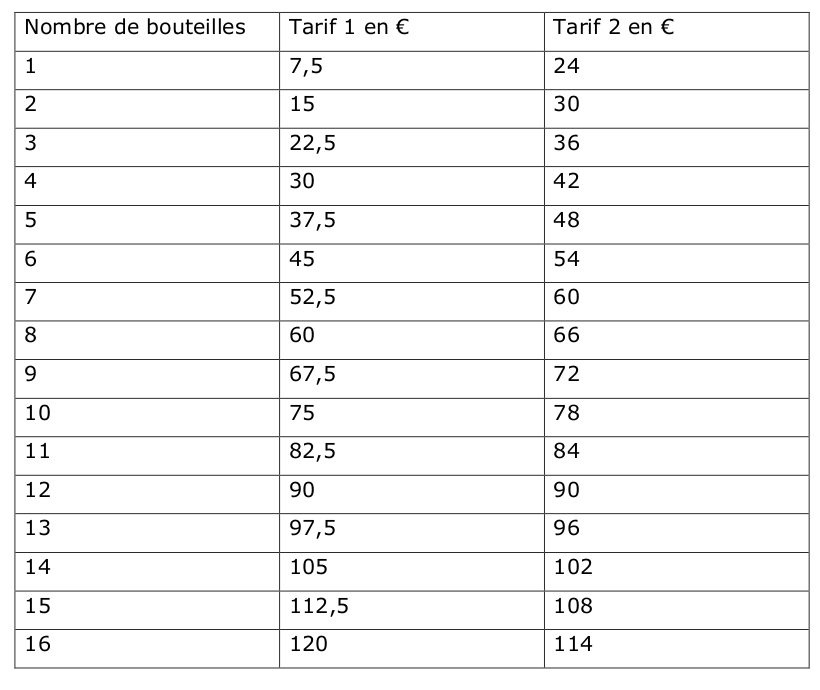
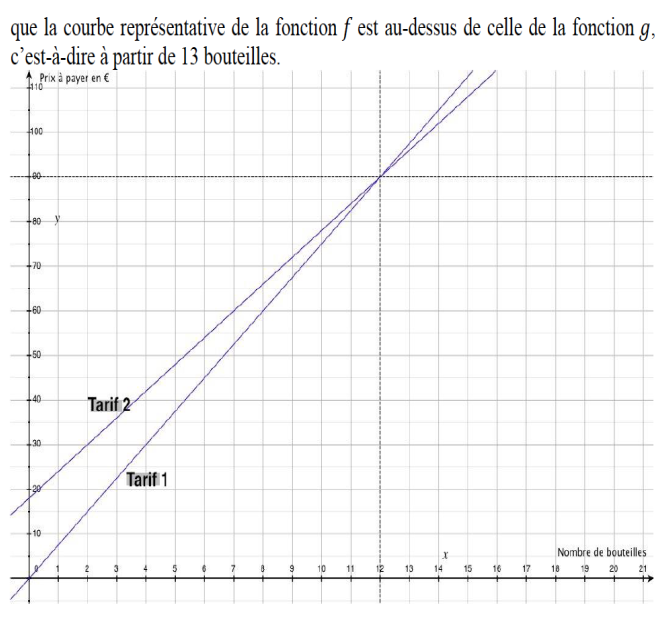
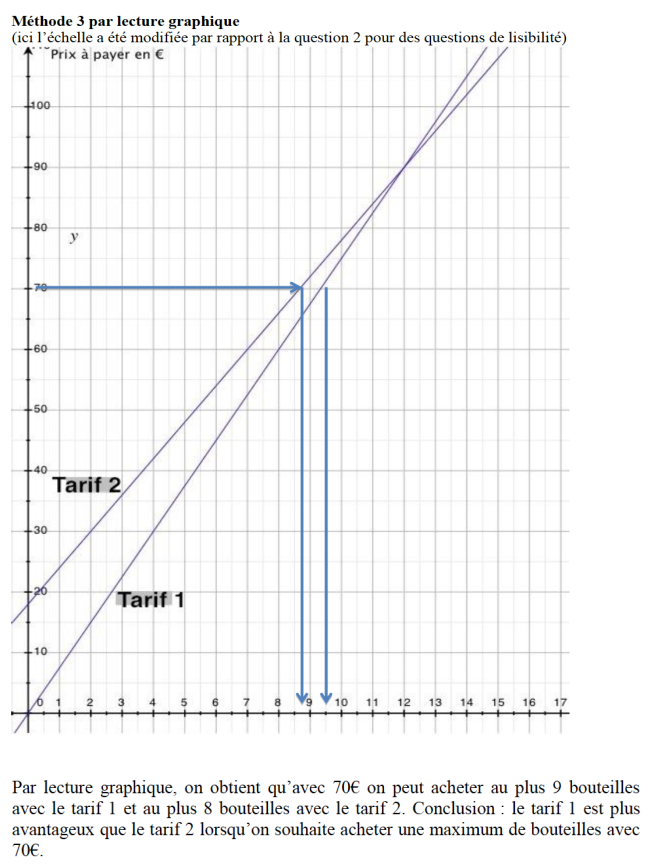
A partir de 13 bouteilles, le tarif 2 est plus avantageux.

Exercice 9
Analyse de travaux d’élèves
1) corrigé de l’exercice
1- On peut faire un tableau

Pour résoudre ce problème de proportionnalité la méthode la plus simple est d’utiliser la linéarité additive. On trouve 10+25=35 livres
2-En utilisant la linéarité multiplicative, on obtient 20m de papier, pour deux fois plus de livres, il faut deux fois plus de papier.
3- Avec 6m de papier, on peut dire que 4x1,5=6 donc le nombre de livres est 10x1,5=15.
Pour trouver 15 livres, on peut également utiliser la propriété des écarts : la différence 10m-4m correspond à la différence 25- 10=15 livres.

2) Procédures utilisées par les élèves :

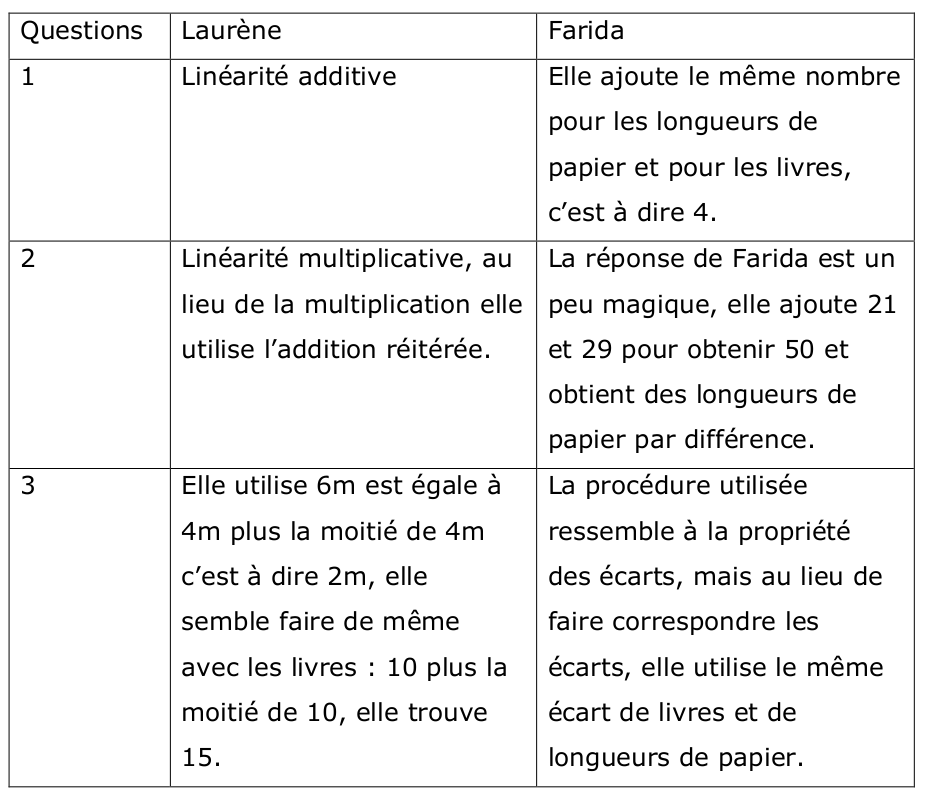3) Liste des erreurs de ces deux élèves.

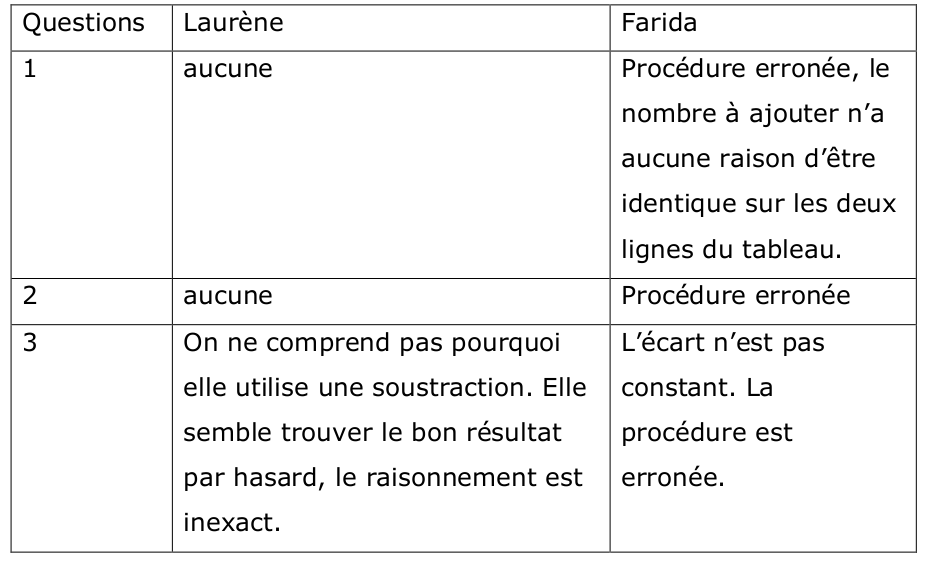
Exercice 10
1)

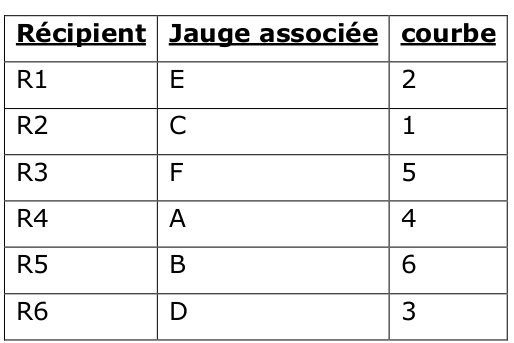
2) La formule pour trouver le volume d'un cylindre est :
Π r 2 × h = V
Nous connaissons le volume total, soit 10 litres, c'est-à-dire 10 000 cm 3
(1 m 3 = 1 000 litres).
Si le diamètre du tube est égal à 16 cm, son rayon est égal à 8 cm.
Si on arrondit au centimètre, on obtient une hauteur de 50 cm.