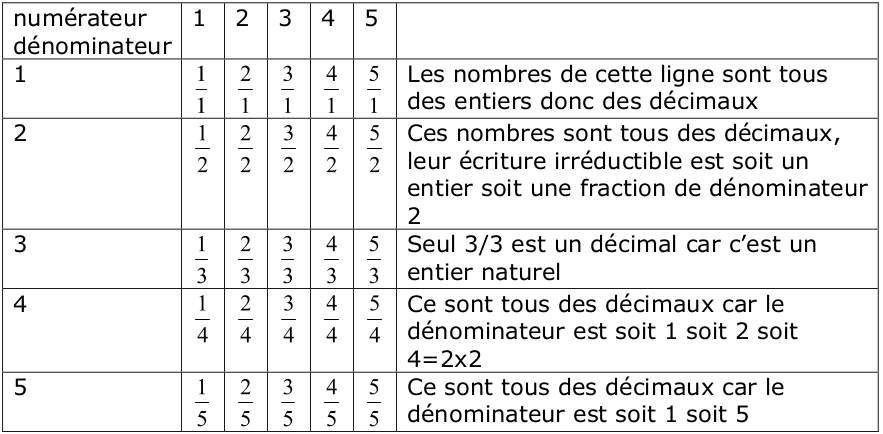
Exercice 1

Voici un extrait des programmes concernant les nombres entiers, rationnels et décimaux, il faut l’avoir lu pour le concours.

 

1) La compétence visée est : « Etre capable d’utiliser des fractions simples dans un cas simple de partage et/ou de codage de mesures de longueurs ».

2) On peut distinguer les procédures du groupe émetteur et du groupe récepteur.

Pour le groupe émetteur :

• reporter la bande-unité un certain nombre de fois puis « coder » la partie supplémentaire, le reliquat non entier.
• penser à plier la bande unité en 2, en 4 ou en 8 pour exprimer la longueur supplémentaire grâce à un fractionnement de l’unité.
• savoir exprimer un message sous la forme « deux bandes et une demi bande », par exemple.

Pour le groupe récepteur :

• comprendre le message
• savoir mesurer les segments
• trouver le segment qui a même mesure que le segment décrit.
   

3) a) La principale difficulté pour les élèves est de penser à partager en parts égales la bande unité et de nommer la part obtenue. En effet, les élèves ont tendance à confondre le nombre de fois où ils ont plié avec le nombre de parts égales de la bande unité.

    b) Les élèves annoncent que la longueur est comprise entre deux entiers, entre 2 et 3 par exemple ou bien ils diront que c’est un peu plus de 2, un peu moins de 3. Le vocabulaire des fractions ne peut s’inventer, il peut être vu dans une séance précédente.

4)

• Si le message est correct : Le groupe récepteur doit comprendre les messages (de découverte) et peut avoir les mêmes difficultés de mesurage des segments.
• Si le message n’est pas correct : les élèves peuvent choisir un segment s’approchant le plus de la description et ainsi se tromper ou en oublier.
   

5)

• L’enseignant peut dire aux élèves qu’ils ont le droit de plier la bande. Il devra vérifier que les parts obtenues sont des parts égales.
• A la fin de la première séance on peut faire une synthèse avec des différents messages pour distinguer ce qui sont corrects et ceux qui ne le sont pas. Il ne faut pas hésiter à faire deux séances sur l’apprentissage de la compétence visée.
   

Exercice 2 DIDACTIQUE (aspect ordinal des fractions)

1. Un objectif de la partie 1 est de lire la fraction qui correspond au point et de placer des fractions sur une droite graduée. Il s’agit d’utiliser les tiers, les cinquièmes et les dixièmes de l’unité. -Dans la partie 2, le partage en parts égales de l’unité est différentes, l’unité est partagée en dix parts égales.
   L’objectif de la partie 2 de placer des nombres décimaux sur des droites graduées, l’unité étant partagée en dix ou en cent parts égales.
    
2. Pour le point B , les abscisses possibles sont :

Pour le point F, les abscisses possibles sont :

3- Les auteurs attendent que les élèves placent le point K sur le premier axe, mais il faut réaliser que est la moitié de

Les élèves peuvent plaçer le point K sur le deuxième ou le troisième axe.

Sur le deuxième axe, l’élève peut par exemple compter dix graduations et arriver à 2.

Sur le troisième axe, l’élève peut confondre le rôle du numérateur et celui du dénominateur et compter 6 graduations.
 

4- La différence entre les questions 1 et 2 de la partie 2 , il y a une graduation en dixièmes puis en centièmes.

5- Les erreurs possibles pour la question 2 de la partie 2 , l’élève peut ne pas tenir compte des nombres placés et de la graduation, il peut répondre G : 3,64, il compte dans le mauvais sens, à l’envers.

Exercice 3

Quand les écritures possèdent une particularité, utilisez-là !

Simplifier une fraction, c’est diviser numérateur et dénominateur par un même nombre.

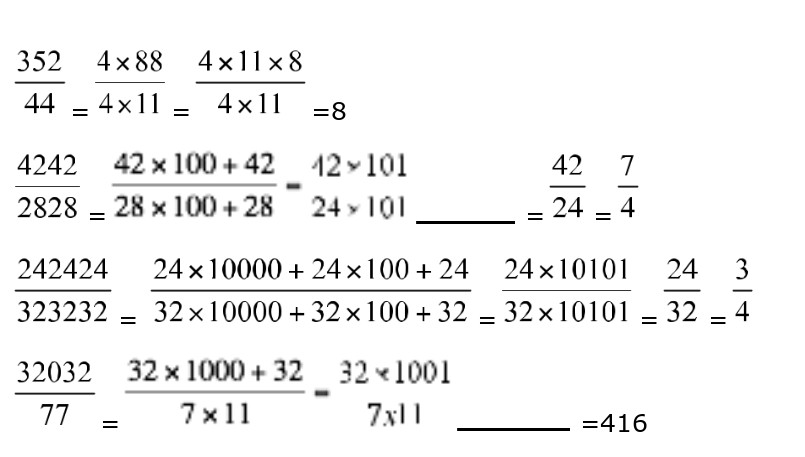
B est inférieur à A, en effet, une méthode consiste à faire la différence. On obtient en faisant la différence terme à terme (ce n’est pas une obligation mais c’est pratique)
 

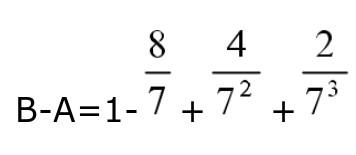
Exercice 4 :

 

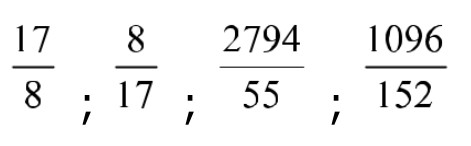
Méthode :

• Pour reconnaître un nombre décimal avec son écriture fractionnaire, on commence par simplifier la fraction de façon à la rendre irréductible.
   
• Ensuite, on décompose le dénominateur en facteurs premiers, c’est-à-dire sous forme de produit avec des nombres premiers comme : 2, 3, 5, 7, 11, 13 etc…

Si le dénominateur ne comporte que des 2 et des 5 dans la décomposition en nombres premiers c’est un nombre décimal.
 

Ainsi dix-sept huitièmes est un nombre décimal car la fraction est irréductible et son dénominateur s’écrit : 8=2x2x2.
 

non décimal.

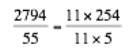
C’est bien un nombre décimal car après simplification, on obtient au dénominateur 5.

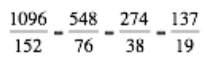
qui n’est pas un nombre décimal.

Conclusion :

est un nombre décimal car la fraction est irréductible et de dénominateur 8 (qui est une puissance de 2)

  est un nombre rationnel non décimal car la fraction est irréductible et de dénominateur 17

 

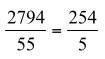 est un nombre décimal (qui est un rationnel, car un nombre décimal est un rationnel (car la fraction irréductible est de dénominateur 5 (qui est une puissance de 5)

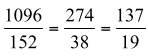 est un nombre rationnel non décimal car la fraction est irréductible et de dénominateur 19

 

Exercice 5

Pour ajouter deux fractions, on commence par chercher un dénominateur commun.

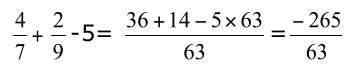
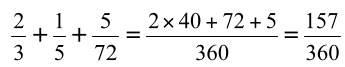 le plus petit commun multiple de 3, 5, 72 est 360.

Enfin 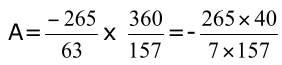qui est irréductible ce n’est pas un nombre
décimal, car le dénominateur comporte un 7 dans sa décomposition en facteurs premiers.

 

Exercice 6

Les nombres entiers sont des nombres décimaux, donc 5 et 0 sont des décimaux.

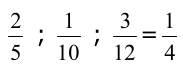 et 0,25 sont des nombres rationnels et décimaux car leur écriture fractionnaire irréductible ne comporte que des 2 et des 5.

 et 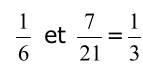 sont des rationnels non décimaux car leur écriture fractionnaire irréductible comporte 3 au dénominateur.

 

Exercice 7

 

Exercice 8

 

 

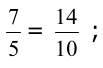
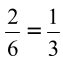impossible de trouver une fraction décimale, écriture à virgule arrondi par excès est 0,34.

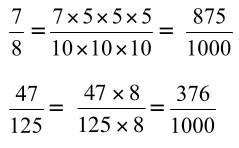
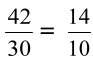  j’ai simplifié par 3.

ne peut être égal à une fraction décimale. Valeur approchée par excès 2,15.

 

Exercice 9 :

 

    1) Un nombre décimal (ou une fraction décimale) compris entre 3,0001 et 3,01 peut s’obtenir en écrivant 3,0001 et 3,0100. On peut alors proposer 3,0002 ; 3,0003 ; ….3,0099 avec que des zéros dans l’écriture décimale à partir du 5° rang.

    2) Recherche d’un nombre non décimal compris entre 3,00001 et 3,01.

On peut écrire ces deux nombres ainsi 3,00001 et 3,01000 cet fois-ci on cherche un nombre non décimal par exemple
3,00001333333333333…. Infinité de 3 après le 1; soit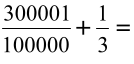

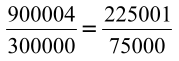
    3) une fraction (un rationnel) entre 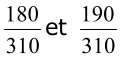  s’obtient facilement par exemple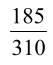

    4) une fraction (un rationnel) entre 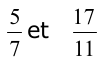 peut s’obtenir après réduction au même dénominateur et en appliquant la méthode précédente

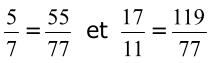 ainsi tout rationnel de numérateur compris entre 55 et 119 et dénominateur 77 convient.

 

Exercice 10

Le nombre de dixièmes est 233.

Le chiffre des centièmes est donc 6

Le chiffre des millièmes est 3.

Le chiffre des dizaines est 3 comme celui des dix-millièmes.

Réponse : 23,3633